Local quantum field theory
Encyclopedia
The Haag-Kastler axiomatic framework for quantum field theory
, named after Rudolf Haag
and Daniel Kastler
, is an application to local quantum physics of C*-algebra theory. It is therefore also known as Algebraic Quantum Field Theory (AQFT). The axioms are stated in terms of an algebra given for every open set in Minkowski space
, and mappings between those.
Let Mink be the category
of open subsets of Minkowski space M with inclusion map
s as morphism
s. We are given a covariant functor
from Mink to uC*alg, the category of unital C* algebras, such that every morphism in Mink maps to a monomorphism
in uC*alg (isotony).
The Poincaré group
acts continuously on Mink. There exists a pullback
of this action
, which is continuous in the norm topology of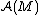
(Poincaré covariance).
Minkowski space has a causal structure
. If an open set
V lies in the causal complement of an open set U, then the image
of the maps
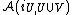
and
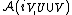
commute (spacelike commutativity). If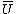
is the causal completion of an open set U, then 
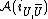is an isomorphism
(primitive causality).
A state
with respect to a C*-algebra is a positive linear functional
over it with unit norm
. If we have a state over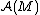
, we can take the "partial trace
" to get states associated with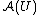
for each open set via the net monomorphism. It's easy to show the states over the open sets form a presheaf structure.
According to the GNS construction, for each state, we can associate a Hilbert space
representation
of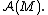
Pure states correspond to irreducible representations and mixed states correspond to reducible representations. Each irreducible (up to equivalence
) is called a superselection sector
. We assume there is a pure state called the vacuum
such that the Hilbert space associated with it is a unitary representation
of the Poincaré group
compatible with the Poincaré covariance of the net such that if we look at the Poincaré algebra, the spectrum with respect to energy-momentum (corresponding to spacetime translations) lies on and in the positive light cone
. This is the vacuum sector.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, named after Rudolf Haag
Rudolf Haag
Rudolf Haag is a German physicist. He is best known for his contributions to the algebraic formulation of axiomatic quantum field theory, namely the Haag-Kastler axioms...
and Daniel Kastler
Daniel Kastler
Daniel Kastler is a French theoretical physicist, working at University of Aix-Marseille on non-commutative geometry.He is best known for his 1964 article with Rudolf Haag on algebraic quantum field theory, which is one of the ....
, is an application to local quantum physics of C*-algebra theory. It is therefore also known as Algebraic Quantum Field Theory (AQFT). The axioms are stated in terms of an algebra given for every open set in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, and mappings between those.
Let Mink be the category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of open subsets of Minkowski space M with inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
s as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s. We are given a covariant functor
from Mink to uC*alg, the category of unital C* algebras, such that every morphism in Mink maps to a monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
in uC*alg (isotony).
The Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
acts continuously on Mink. There exists a pullback
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
of this action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
, which is continuous in the norm topology of
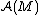(Poincaré covariance).Minkowski space has a causal structure
Causal structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
. If an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
V lies in the causal complement of an open set U, then the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the maps
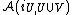
and
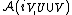
commute (spacelike commutativity). If
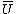is the causal completion of an open set U, then 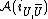is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
(primitive causality).
A state
State (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
with respect to a C*-algebra is a positive linear functional
Positive linear functional
In mathematics, especially in functional analysis, a positive linear functional on an ordered vector space is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds thatf\geq 0....
over it with unit norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. If we have a state over
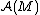, we can take the "partial tracePartial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
" to get states associated with
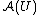for each open set via the net monomorphism. It's easy to show the states over the open sets form a presheaf structure.According to the GNS construction, for each state, we can associate a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of
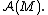Pure states correspond to irreducible representations and mixed states correspond to reducible representations. Each irreducible (up to equivalenceEquivalence
Equivalence or equivalent may refer to:*In chemistry:**Equivalent **Equivalence point**Equivalent weight*In computing:**Turing equivalence *In ethics:**Moral equivalence*In history:...
) is called a superselection sector
Superselection sector
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
. We assume there is a pure state called the vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
such that the Hilbert space associated with it is a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
compatible with the Poincaré covariance of the net such that if we look at the Poincaré algebra, the spectrum with respect to energy-momentum (corresponding to spacetime translations) lies on and in the positive light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
. This is the vacuum sector.
Suggested reading
- Haag, RudolfRudolf HaagRudolf Haag is a German physicist. He is best known for his contributions to the algebraic formulation of axiomatic quantum field theory, namely the Haag-Kastler axioms...
(1992). Local Quantum Physics: Fields, Particles, Algebras. Springer.
External links
- Local Quantum Physics Crossroads - A network of scientists working on Local Quantum Physics
- Algebraic Quantum Field Theory - AQFT resources at the University of Hamburg