
Local Euler characteristic formula
Encyclopedia
In the mathematical field of Galois cohomology
, the local Euler characteristic formula is a result due to John Tate
that computes the Euler characteristic
of the group cohomology
of the absolute Galois group
GK of a non-archimedean local field K.
of GK is two, Hi(K, M) = 0 for i ≥ 3. Therefore, the Euler characteristic only involves the groups with i = 0, 1, 2.
of finite order
m. The Euler characteristic of M is defined to be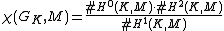
(the ith cohomology groups for i ≥ 3 appear tacitly as their sizes are all one).
Let R denote the ring of integers
of K. Tate's result then states that if m is relatively prime to the characteristic
of K, then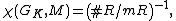
i.e. the inverse of the order of the quotient ring
R/mR.
Two special cases worth singling out are the following. If the order of M is relatively prime to the characteristic of the residue field
of K, then the Euler characteristic is one. If K is a finite extension of the p-adic numbers
Qp, and if vp denotes the p-adic valuation
, then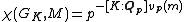
where [K:Qp] is the degree
of K over Qp.
The Euler characteristic can be rewritten, using local Tate duality
, as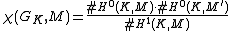
where M′ is the local Tate dual of M.
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
, the local Euler characteristic formula is a result due to John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
that computes the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
of the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
GK of a non-archimedean local field K.
Statement
Let K be a non-archimedean local field, let Ks denote a separable closure of K, let GK = Gal(Ks/K) be the absolute Galois group of K, and let Hi(K, M) denote the group cohomology of GK with coefficients in M. Since the cohomological dimensionCohomological dimension
In abstract algebra, cohomological dimension is an invariant which measures the homological complexity of representations of a group. It has important applications in geometric group theory, topology, and algebraic number theory....
of GK is two, Hi(K, M) = 0 for i ≥ 3. Therefore, the Euler characteristic only involves the groups with i = 0, 1, 2.
Case of finite modules
Let M be a GK-moduleGalois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
of finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
m. The Euler characteristic of M is defined to be
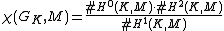
(the ith cohomology groups for i ≥ 3 appear tacitly as their sizes are all one).
Let R denote the ring of integers
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
of K. Tate's result then states that if m is relatively prime to the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of K, then
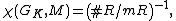
i.e. the inverse of the order of the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R/mR.
Two special cases worth singling out are the following. If the order of M is relatively prime to the characteristic of the residue field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
of K, then the Euler characteristic is one. If K is a finite extension of the p-adic numbers
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
Qp, and if vp denotes the p-adic valuation
P-adic order
In number theory, for a given prime number p, the p-adic order or additive p-adic valuation of a number n is the highest exponent ν such that pν divides n. It is commonly abbreviated νp. The most important application of the p-adic order is in constructing the field of p-adic numbers...
, then
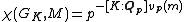
where [K:Qp] is the degree
Degree of a field extension
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
of K over Qp.
The Euler characteristic can be rewritten, using local Tate duality
Local Tate duality
In Galois cohomology, local Tate duality is a duality for Galois modules for the absolute Galois group of a non-archimedean local field. It is named after John Tate who first proved it. It shows that the dual of such a Galois module is the Tate twist of usual linear dual...
, as
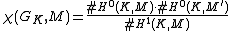
where M′ is the local Tate dual of M.

