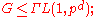List of transitive finite linear groups
Encyclopedia
In mathematics
, especially in areas of abstract algebra
and finite geometry
, the list of transitive finite linear groups is an important classification of certain highly symmetric actions
of finite group
s on vector space
s.
The solvable
finite 2-transitive group
s were classified by Bertram Huppert
. The classification of finite simple groups
made possible the complete classification of finite doubly transitive permutation groups. This is a result by Christoph Hering. A finite 2-transitive group has a socle
that is either a vector space over a finite field
or a non-abelian primitive simple group
; groups of the latter kind are almost simple groups and described elsewhere. This article provides a complete list of the finite 2-transitive groups whose socle is elementary abelian
.
Let
be a prime, and 
a subgroup of the general linear group
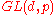acting transitively on the nonzero vectors of the d-dimensional vector space 
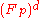over the finite field 
with p elements.
Notice that the exceptional group of Lie type
G2(q) is usually constructed as the automorphism groups of the split octonion
s. Hence, it has a natural representation
as a subgroup of the 7-dimensional orthogonal group
O(7, q). If q is even, then the underlying quadratic form
polarizes to a degenerate symplectic form. Factoring out with the radical, one obtains an isomorphism
between O(7, q) and the symplectic group
Sp(6, q). The subgroup of Sp(6, q) which corresponds to G2(q)′ is transitive.
In fact, for q>2, the group G2(q) = G2(q)′ is simple. If q=2 then G2(2)′ ≅ PSU(3,3) is simple with index 2 in G2(2).
, this normal subgroup is denoted by G0 and are written in the third column of the table. The notation 21+4 stands for the extraspecial group of order 32.
All but one of the sporadic transitive linear groups
yield a primitive permutation group 
of degree at most 2499. In the computer algebra programs GAP
and MAGMA
, these groups can be accessed with the command
. This number is given in the last column of the following table.
Seven of these groups are sharply transitive, these groups were found by Hans Julius Zassenhaus
and are also known as the multiplicative groups of the Zassenhaus near-fields. These groups are marked by a star in the table.
This list is not explicitly contained in Hering's paper. Many books and papers give a list of these groups, some of them an incomplete one. For example, Cameron's book misses the groups in line 5 of the table.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in areas of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and finite geometry
Finite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
, the list of transitive finite linear groups is an important classification of certain highly symmetric actions
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s on vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s.
The solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
finite 2-transitive group
2-transitive group
In the area of abstract algebra known as group theory, a 2-transitive group is a transitive permutation group in which a point stabilizer acts transitively on the remaining points. Every 2-transitive group is a primitive group, but not conversely. Every Zassenhaus group is 2-transitive, but not...
s were classified by Bertram Huppert
Bertram Huppert
Bertram Huppert is a German mathematician specializing in group theory and the representation theory of finite groups. His Endliche Gruppen is an influential textbook in group theory, and he has over 50 doctoral descendants.-Education:Bertram Huppert went to school in Bonn from 1934 until 1945...
. The classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
made possible the complete classification of finite doubly transitive permutation groups. This is a result by Christoph Hering. A finite 2-transitive group has a socle
Socle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
that is either a vector space over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
or a non-abelian primitive simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
; groups of the latter kind are almost simple groups and described elsewhere. This article provides a complete list of the finite 2-transitive groups whose socle is elementary abelian
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
.
Let
be a prime, and a subgroup of the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
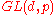acting transitively on the nonzero vectors of the d-dimensional vector space 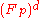over the finite field with p elements.Infinite classes
There are four infinite classes of finite transitive linear groups.
Notice that the exceptional group of Lie type
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
G2(q) is usually constructed as the automorphism groups of the split octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s. Hence, it has a natural representation
Representation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
as a subgroup of the 7-dimensional orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(7, q). If q is even, then the underlying quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
polarizes to a degenerate symplectic form. Factoring out with the radical, one obtains an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between O(7, q) and the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(6, q). The subgroup of Sp(6, q) which corresponds to G2(q)′ is transitive.
In fact, for q>2, the group G2(q) = G2(q)′ is simple. If q=2 then G2(2)′ ≅ PSU(3,3) is simple with index 2 in G2(2).
Sporadic finite transitive linear groups
These groups are usually classified by some typical normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, this normal subgroup is denoted by G0 and are written in the third column of the table. The notation 21+4 stands for the extraspecial group of order 32.
All but one of the sporadic transitive linear groups
yield a primitive permutation group of degree at most 2499. In the computer algebra programs GAPGAP computer algebra system
GAP is a computer algebra system for computational discrete algebra with particular emphasis on computational group theory.-History:...
and MAGMA
MAGMA
MAGMA Gießereitechnologie GmbH develops and markets software for casting process simulation. The software is used world-wide by foundries, casting buyers and designers. In addition to the simulation software MAGMASOFT®, respectively MAGMA5, the product and service portfolio includes engineering...
, these groups can be accessed with the command
PrimitiveGroup(p^d,k); where the number k is the primitive identification of . This number is given in the last column of the following table.Seven of these groups are sharply transitive, these groups were found by Hans Julius Zassenhaus
Hans Julius Zassenhaus
Hans Julius Zassenhaus was a German mathematician, known for work in many parts of abstract algebra, and as a pioneer of computer algebra....
and are also known as the multiplicative groups of the Zassenhaus near-fields. These groups are marked by a star in the table.
Condition on  |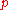
Condition on  |
 |
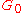Primitive identification of  |
|---|---|---|---|
 |
 |
 |
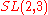15*, 18, 19 |
 |
 |
 |
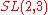25*, 29 |
 |
 |
 |
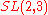39*, 42 |
 |
 |
 |
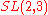59* |
 |
 |
 |
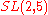124, 126, 127, 128 |
 |
 |
 |
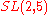56*, 57 |
 |
 |
 |
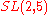86 |
 |
 |
 |
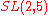106*, 110 |
 |
 |
 |
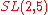no id, * (regular) |
 |
 |
 |
71, 90, 99, 129, 130 |
 |
 |
 |
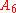16, 17 |
 |
 |
 |
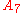20 |
 |
 |
 |
396 |
This list is not explicitly contained in Hering's paper. Many books and papers give a list of these groups, some of them an incomplete one. For example, Cameron's book misses the groups in line 5 of the table.