
Linear cryptanalysis
Encyclopedia
In cryptography
, linear cryptanalysis is a general form of cryptanalysis
based on finding affine
approximations to the action of a cipher
. Attacks have been developed for block cipher
s and stream cipher
s. Linear cryptanalysis is one of the two most widely used attacks on block ciphers; the other being differential cryptanalysis
.
The discovery is attributed to Mitsuru Matsui
, who first applied the technique to the FEAL
cipher (Matsui and Yamagishi, 1992). Subsequently, Matsui published an attack on the Data Encryption Standard
(DES), eventually leading to the first experimental cryptanalysis of the cipher reported in the open community (Matsui, 1993; 1994). The attack on DES is not generally practical, requiring 243 known plaintexts
.
A variety of refinements to the attack have been suggested, including using multiple linear approximations or incorporating non-linear expressions, leading to a generalized partitioning cryptanalysis
. Evidence of security against linear cryptanalysis is usually expected of new cipher designs.

In an ideal cipher, any linear equation relating plaintext, ciphertext and key bits would hold with probability 1/2. Since the equations dealt with in linear cryptanalysis will vary in probability, they are more accurately referred to as linear approximations.
The procedure for constructing approximations is different for each cipher. In the most basic type of block cipher, a substitution-permutation network
, analysis is concentrated primarily on the S-boxes, the only nonlinear part of the cipher (i.e. the operation of an S-box cannot be encoded in a linear equation). For small enough S-boxes, it is possible to enumerate every possible linear equation relating the S-box's input and output bits, calculate their biases and choose the best ones. Linear approximations for S-boxes then must be combined with the cipher's other actions, such as permutation and key mixing, to arrive at linear approximations for the entire cipher. The piling-up lemma
is a useful tool for this combination step. There are also techniques for iteratively improving linear approximations (Matsui 1994).
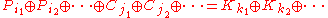
we can then apply a straightforward algorithm (Matsui's Algorithm 2), using known plaintext-ciphertext pairs, to guess at the values of the key bits involved in the approximation.
For each set of values of the key bits on the right-hand side (referred to as a partial key), count how many times the approximation holds true over all the known plaintext-ciphertext pairs; call this count T. The partial key whose T has the greatest absolute difference
from half the number of plaintext-ciphertext pairs is designated as the most likely set of values for those key bits. This is because it is assumed that the correct partial key will cause the approximation to hold with a high bias. The magnitude of the bias is significant here, as opposed to the magnitude of the probability itself.
This procedure can be repeated with other linear approximations, obtaining guesses at values of key bits, until the number of unknown key bits is low enough that they can be attacked with brute force.
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, linear cryptanalysis is a general form of cryptanalysis
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
based on finding affine
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
approximations to the action of a cipher
Cipher
In cryptography, a cipher is an algorithm for performing encryption or decryption — a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. In non-technical usage, a “cipher” is the same thing as a “code”; however, the concepts...
. Attacks have been developed for block cipher
Block cipher
In cryptography, a block cipher is a symmetric key cipher operating on fixed-length groups of bits, called blocks, with an unvarying transformation. A block cipher encryption algorithm might take a 128-bit block of plaintext as input, and output a corresponding 128-bit block of ciphertext...
s and stream cipher
Stream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
s. Linear cryptanalysis is one of the two most widely used attacks on block ciphers; the other being differential cryptanalysis
Differential cryptanalysis
Differential cryptanalysis is a general form of cryptanalysis applicable primarily to block ciphers, but also to stream ciphers and cryptographic hash functions. In the broadest sense, it is the study of how differences in an input can affect the resultant difference at the output...
.
The discovery is attributed to Mitsuru Matsui
Mitsuru Matsui
is a Japanese cryptographer and senior researcher for Mitsubishi Electric Company. While researching error-correcting codes in 1990, Matsui was inspired by Biham and Shamir's differential cryptanalysis, and discovered the technique of linear cryptanalysis, published in 1993. Differential and linear...
, who first applied the technique to the FEAL
FEAL
In cryptography, FEAL is a block cipher proposed as an alternative to the Data Encryption Standard , and designed to be much faster in software. The Feistel based algorithm was first published in 1987 by Akihiro Shimizu and Shoji Miyaguchi from NTT...
cipher (Matsui and Yamagishi, 1992). Subsequently, Matsui published an attack on the Data Encryption Standard
Data Encryption Standard
The Data Encryption Standard is a block cipher that uses shared secret encryption. It was selected by the National Bureau of Standards as an official Federal Information Processing Standard for the United States in 1976 and which has subsequently enjoyed widespread use internationally. It is...
(DES), eventually leading to the first experimental cryptanalysis of the cipher reported in the open community (Matsui, 1993; 1994). The attack on DES is not generally practical, requiring 243 known plaintexts
Known-plaintext attack
The known-plaintext attack is an attack model for cryptanalysis where the attacker has samples of both the plaintext , and its encrypted version . These can be used to reveal further secret information such as secret keys and code books...
.
A variety of refinements to the attack have been suggested, including using multiple linear approximations or incorporating non-linear expressions, leading to a generalized partitioning cryptanalysis
Partitioning cryptanalysis
In cryptography, partitioning cryptanalysis is a form of cryptanalysis for block ciphers. Developed by Carlo Harpes in 1995, the attack is a generalization of linear cryptanalysis. Harpes originally replaced the bit sums of linear cryptanalysis with more general balanced Boolean functions...
. Evidence of security against linear cryptanalysis is usually expected of new cipher designs.
Overview
There are two parts to linear cryptanalysis. The first is to construct linear equations relating plaintext, ciphertext and key bits that have a high bias; that is, whose probabilities of holding (over the space of all possible values of their variables) are as close as possible to 0 or 1. The second is to use these linear equations in conjunction with known plaintext-ciphertext pairs to derive key bits.Constructing linear equations
For the purposes of linear cryptanalysis, a linear equation expresses the equality of two expressions which consist of binary variables combined with the exclusive-or (XOR) operation. For example, the following equation, from a hypothetical cipher, states the XOR sum of the first and third plaintext bits (as in a block cipher's block) and the first ciphertext bit is equal to the second bit of the key:
In an ideal cipher, any linear equation relating plaintext, ciphertext and key bits would hold with probability 1/2. Since the equations dealt with in linear cryptanalysis will vary in probability, they are more accurately referred to as linear approximations.
The procedure for constructing approximations is different for each cipher. In the most basic type of block cipher, a substitution-permutation network
Substitution-permutation network
In cryptography, an SP-network, or substitution-permutation network , is a series of linked mathematical operations used in block cipher algorithms such as AES .Other ciphers that use SPNs are 3-Way, SAFER, SHARK, and Square....
, analysis is concentrated primarily on the S-boxes, the only nonlinear part of the cipher (i.e. the operation of an S-box cannot be encoded in a linear equation). For small enough S-boxes, it is possible to enumerate every possible linear equation relating the S-box's input and output bits, calculate their biases and choose the best ones. Linear approximations for S-boxes then must be combined with the cipher's other actions, such as permutation and key mixing, to arrive at linear approximations for the entire cipher. The piling-up lemma
Piling-up lemma
In cryptanalysis, the piling-up lemma is a principle used in linear cryptanalysis to construct linear approximation to the action of block ciphers...
is a useful tool for this combination step. There are also techniques for iteratively improving linear approximations (Matsui 1994).
Deriving key bits
Having obtained a linear approximation of the form: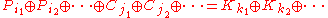
we can then apply a straightforward algorithm (Matsui's Algorithm 2), using known plaintext-ciphertext pairs, to guess at the values of the key bits involved in the approximation.
For each set of values of the key bits on the right-hand side (referred to as a partial key), count how many times the approximation holds true over all the known plaintext-ciphertext pairs; call this count T. The partial key whose T has the greatest absolute difference
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
from half the number of plaintext-ciphertext pairs is designated as the most likely set of values for those key bits. This is because it is assumed that the correct partial key will cause the approximation to hold with a high bias. The magnitude of the bias is significant here, as opposed to the magnitude of the probability itself.
This procedure can be repeated with other linear approximations, obtaining guesses at values of key bits, until the number of unknown key bits is low enough that they can be attacked with brute force.

