Linear-quadratic regulator
Encyclopedia
The theory of optimal control
is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equation
s and the cost is described by a quadratic
functional
is called the LQ problem. One of the main results in the theory is that the solution is provided by the linear-quadratic regulator (LQR), a feedback controller whose equations are given below. The LQR is an important part of the solution to the LQG problem
. Like the LQR problem itself, the LQG problem is one of the most fundamental problems in control theory
.
In effect, the LQR algorithm takes care of the tedious work done by the control systems engineer in optimizing the controller. However, the engineer still needs to specify the weighting factors and compare the results with the specified design goals. Often this means that controller synthesis will still be an iterative process where the engineer judges the produced "optimal" controllers through simulation and then adjusts the weighting factors to get a controller more in line with the specified design goals.
The LQR algorithm is, at its core, just an automated way of finding an appropriate state-feedback controller
. And as such it is not uncommon to find that control engineers prefer alternative methods like full state feedback
(also known as pole placement) to find a controller over the use of the LQR algorithm. With these the engineer has a much clearer linkage between adjusted parameters and the resulting changes in controller behavior. Difficulty in finding the right weighting factors limits the application of the LQR based controller synthesis.
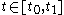, described by
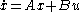
with a quadratic cost function defined as
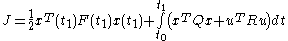
the feedback control law that minimizes the value of the cost is
where
is given by
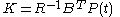
and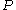
is found by solving the continuous time Riccati differential equation.
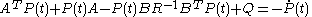
The first order conditions for Jmin are
(i) State equation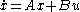
(ii) Co-state equation
(iii) Stationary equation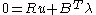
(iv) Boundary conditions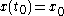
and
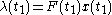
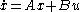
with a cost functional defined as
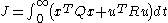
the feedback control law that minimizes the value of the cost is
where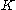
is given by
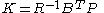
and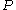
is found by solving the continuous time algebraic Riccati equation
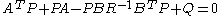
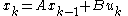
with a performance index defined as
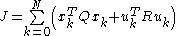
the optimal control sequence minimizing the performance index is given by
where
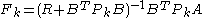
and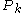
is found iteratively backwards in time by the dynamic Riccati equation
from initial condition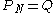
.
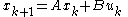
with a performance index defined as
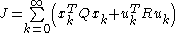
the optimal control sequence minimizing the performance index is given by
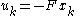
where
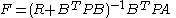
and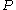
is the unique positive definite solution to the discrete time algebraic Riccati equation
(DARE)
.
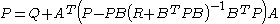Note that one way to solve this equation is by iterating the dynamic Riccati equation of the finite-horizon case until it converges.
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s and the cost is described by a quadratic
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
is called the LQ problem. One of the main results in the theory is that the solution is provided by the linear-quadratic regulator (LQR), a feedback controller whose equations are given below. The LQR is an important part of the solution to the LQG problem
Linear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
. Like the LQR problem itself, the LQG problem is one of the most fundamental problems in control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
.
General description
In layman's terms this means that the settings of a (regulating) controller governing either a machine or process (like an airplane or chemical reactor) are found by using a mathematical algorithm that minimizes a cost function with weighting factors supplied by a human (engineer). The "cost" (function) is often defined as a sum of the deviations of key measurements from their desired values. In effect this algorithm therefore finds those controller settings that minimize the undesired deviations, like deviations from desired altitude or process temperature. Often the magnitude of the control action itself is included in this sum so as to keep the energy expended by the control action itself limited.In effect, the LQR algorithm takes care of the tedious work done by the control systems engineer in optimizing the controller. However, the engineer still needs to specify the weighting factors and compare the results with the specified design goals. Often this means that controller synthesis will still be an iterative process where the engineer judges the produced "optimal" controllers through simulation and then adjusts the weighting factors to get a controller more in line with the specified design goals.
The LQR algorithm is, at its core, just an automated way of finding an appropriate state-feedback controller
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
. And as such it is not uncommon to find that control engineers prefer alternative methods like full state feedback
Full state feedback
Full state feedback , or pole placement, is a method employed in feedback control system theory to place the closed-loop poles of a plant in pre-determined locations in the s-plane. Placing poles is desirable because the location of the poles corresponds directly to the eigenvalues of the system,...
(also known as pole placement) to find a controller over the use of the LQR algorithm. With these the engineer has a much clearer linkage between adjusted parameters and the resulting changes in controller behavior. Difficulty in finding the right weighting factors limits the application of the LQR based controller synthesis.
Finite-horizon, continuous-time LQR
For a continuous-time linear system, defined on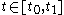, described by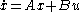with a quadratic cost function defined as
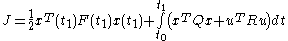
the feedback control law that minimizes the value of the cost is
where
is given by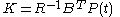and
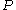is found by solving the continuous time Riccati differential equation.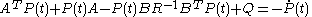The first order conditions for Jmin are
(i) State equation
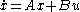
(ii) Co-state equation
(iii) Stationary equation
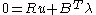
(iv) Boundary conditions
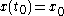
and
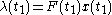
Infinite-horizon, continuous-time LQR
For a continuous-time linear system described by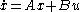with a cost functional defined as
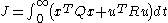
the feedback control law that minimizes the value of the cost is
where
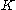is given by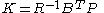and
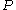is found by solving the continuous time algebraic Riccati equationAlgebraic Riccati equation
The algebraic Riccati equation is either of the following matrix equations:the continuous time algebraic Riccati equation :or the discrete time algebraic Riccati equation :...
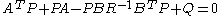
Finite-horizon, discrete-time LQR
For a discrete-time linear system described by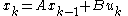with a performance index defined as
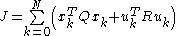
the optimal control sequence minimizing the performance index is given by
where
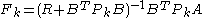
and
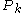is found iteratively backwards in time by the dynamic Riccati equationfrom initial condition
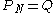.Infinite-horizon, discrete-time LQR
For a discrete-time linear system described by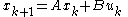with a performance index defined as
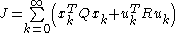
the optimal control sequence minimizing the performance index is given by
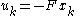
where
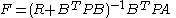
and
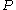is the unique positive definite solution to the discrete time algebraic Riccati equationAlgebraic Riccati equation
The algebraic Riccati equation is either of the following matrix equations:the continuous time algebraic Riccati equation :or the discrete time algebraic Riccati equation :...
(DARE)
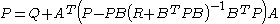.Note that one way to solve this equation is by iterating the dynamic Riccati equation of the finite-horizon case until it converges.