
Costate equations
Encyclopedia
Costate equations are related to the state equations used in optimal control
. They are stated as a vector of first order differential equation
s with the right-hand side being the vector of partial derivative
s of the negative of the Hamiltonian
with respect to the state variables.
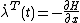
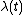 can be interpreted as Lagrange multipliers
can be interpreted as Lagrange multipliers
associated with the state equations. The state equations represent constraints of the minimization problem, and the costate variables represent the marginal cost
of violating those constraints; in economic terms the costate variables are the shadow price
s.
.
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
. They are stated as a vector of first order differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s with the right-hand side being the vector of partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of the negative of the Hamiltonian
Hamiltonian (control theory)
The Hamiltonian of optimal control theory was developed by L. S. Pontryagin as part of his minimum principle. It was inspired by, but is distinct from, the Hamiltonian of classical mechanics. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control...
with respect to the state variables.
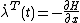
Interpretation
The costate variables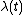 can be interpreted as Lagrange multipliers
can be interpreted as Lagrange multipliersLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
associated with the state equations. The state equations represent constraints of the minimization problem, and the costate variables represent the marginal cost
Marginal cost
In economics and finance, marginal cost is the change in total cost that arises when the quantity produced changes by one unit. That is, it is the cost of producing one more unit of a good...
of violating those constraints; in economic terms the costate variables are the shadow price
Shadow price
In constrained optimization in economics, the shadow price is the instantaneous change per unit of the constraint in the objective value of the optimal solution of an optimization problem obtained by relaxing the constraint...
s.
Solution
The state equations are subject to an initial condition and are solved forwards in time. The costate equations must satisfy a terminal condition and are solved backwards in time, from the final time towards the beginning. For more details see Pontryagin's minimum principlePontryagin's minimum principle
Pontryagin's maximum principle is used in optimal control theory to find the best possible control for taking a dynamical system from one state to another, especially in the presence of constraints for the state or input controls. It was formulated by the Russian mathematician Lev Semenovich...
.

