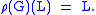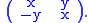Lie–Kolchin theorem
Encyclopedia
In mathematics
, the Lie–Kolchin theorem is a theorem in the representation theory
of linear algebraic group
s; Lie's theorem is the analog for linear Lie algebras.
It states that if G is a connected
and solvable
linear algebraic group
defined over an algebraically closed field
and
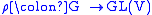
a representation
on a nonzero finite-dimensional vector space
V, then there is a one-dimensional linear subspace L of V such that
That is, ρ(G) has an invariant line L, on which G therefore acts through a one-dimensional representation. This is equivalent to the statement that V contains a nonzero vector v that is a common (simultaneous) eigenvector for all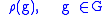
.
Because every (nonzero finite-dimensional) representation of G has a one-dimensional invariant subspace according to the Lie–Kolchin theorem, every irreducible finite-dimensional representation of a connected and solvable linear algebraic group G has dimension one, which is another way to state the Lie–Kolchin theorem.
Lie's theorem states that any nonzero representation of a solvable Lie algebra on a finite dimensional vector space over an algebraically closed field of characteristic 0 has a one-dimensional invariant subspace.
The result for Lie algebras was proved by and for algebraic groups was proved by .
The Borel fixed point theorem generalizes the Lie–Kolchin theorem.
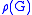has a triangular shape; in other words, the image group 
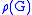is conjugate in GL(n,K) (where n = dim V) to a subgroup of the group T of upper triangular matrices, the standard Borel subgroup
of GL(n,K): the image is simultaneously triangularizable.
The theorem applies in particular to a Borel subgroup
of a semisimple
linear algebraic group
G.
Applying this result repeatedly shows that there is a basis for V such that all elements of the Lie algebra are represented by upper triangular matrices.
This is a generalization of the result of Frobenius that commuting matrices
are simultaneously upper triangularizable, as commuting matrices form an abelian Lie algebra, which is a fortiori solvable.
A consequence of Lie's theorem is that any finite dimensional solvable Lie algebra over a field of characteristic 0 has a nilpotent derived algebra.
, viewed as the set of complex number
s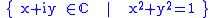
of absolute value one is a one-dimensional commutative (and therefore solvable) linear algebraic group
over the real numbers which has a two-dimensional representation into the special orthogonal group SO(2) without an invariant (real) line. Here the image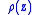
of 
is the orthogonal matrix
For algebraically closed fields of characteristic p>0 Lie's theorem holds provided the dimension of the representation is less than p, but can fail for representations of dimension p. An example is given by the 3-dimensional nilpotent Lie algebra spanned by 1, x, and d/dx acting on the p-dimensional vector space k[x]/(xp), which has no eigenvectors. Taking the semidirect product of this 3-dimensional Lie algebra by the p-dimensional representation (considered as an abelian Lie algebra) gives a solvable Lie algebra whose derived algebra is not nilpotent.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lie–Kolchin theorem is a theorem in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
s; Lie's theorem is the analog for linear Lie algebras.
It states that if G is a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
and solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
defined over an algebraically closed field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and
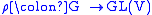
a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
on a nonzero finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, then there is a one-dimensional linear subspace L of V such that
That is, ρ(G) has an invariant line L, on which G therefore acts through a one-dimensional representation. This is equivalent to the statement that V contains a nonzero vector v that is a common (simultaneous) eigenvector for all
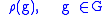.Because every (nonzero finite-dimensional) representation of G has a one-dimensional invariant subspace according to the Lie–Kolchin theorem, every irreducible finite-dimensional representation of a connected and solvable linear algebraic group G has dimension one, which is another way to state the Lie–Kolchin theorem.
Lie's theorem states that any nonzero representation of a solvable Lie algebra on a finite dimensional vector space over an algebraically closed field of characteristic 0 has a one-dimensional invariant subspace.
The result for Lie algebras was proved by and for algebraic groups was proved by .
The Borel fixed point theorem generalizes the Lie–Kolchin theorem.
Triangularization
Sometimes the theorem is also referred to as the Lie–Kolchin triangularization theorem because by induction it implies that with respect to a suitable basis of V the image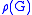 has a triangular shape; in other words, the image group 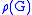is conjugate in GL(n,K) (where n = dim V) to a subgroup of the group T of upper triangular matrices, the standard Borel subgroupBorel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
of GL(n,K): the image is simultaneously triangularizable.
The theorem applies in particular to a Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
of a semisimple
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
G.
Lie's theorem
Lie's theorem states that if V is a finite dimensional vector space over an algebraically closed field of characteristic 0, then for any solvable Lie algebra of endomorphisms of V there is a vector that is an eigenvector for every element of the Lie algebra.Applying this result repeatedly shows that there is a basis for V such that all elements of the Lie algebra are represented by upper triangular matrices.
This is a generalization of the result of Frobenius that commuting matrices
Commuting matrices
In linear algebra, a set of matrices A_1,\ldots,A_k is said to commute if they commute pairwise, meaning A_iA_j = A_jA_i for every pair i, j .- Properties :Commuting matrices over an algebraically closed field are simultaneously triangularizable; indeed,...
are simultaneously upper triangularizable, as commuting matrices form an abelian Lie algebra, which is a fortiori solvable.
A consequence of Lie's theorem is that any finite dimensional solvable Lie algebra over a field of characteristic 0 has a nilpotent derived algebra.
Counter-examples
If the field K is not algebraically closed, the theorem can fail. The standard unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, viewed as the set of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
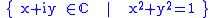of absolute value one is a one-dimensional commutative (and therefore solvable) linear algebraic groupLinear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
over the real numbers which has a two-dimensional representation into the special orthogonal group SO(2) without an invariant (real) line. Here the image
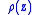of is the orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
For algebraically closed fields of characteristic p>0 Lie's theorem holds provided the dimension of the representation is less than p, but can fail for representations of dimension p. An example is given by the 3-dimensional nilpotent Lie algebra spanned by 1, x, and d/dx acting on the p-dimensional vector space k[x]/(xp), which has no eigenvectors. Taking the semidirect product of this 3-dimensional Lie algebra by the p-dimensional representation (considered as an abelian Lie algebra) gives a solvable Lie algebra whose derived algebra is not nilpotent.