Leibniz formula (determinant)
Encyclopedia
In algebra
, the Leibniz formula expresses the determinant
of a square matrix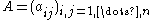
in terms of permutations of the matrix elements. Named in honor of Gottfried Leibniz
, the formula is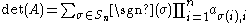
for an n×n matrix, where sgn is the sign function
of permutation
s in the permutation group
Sn, which returns +1 and −1 for even and odd permutations
, respectively.
Another common notation used for the formula is in terms of the Levi-Civita symbol
and makes use of the Einstein summation notation, where it becomes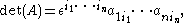
which may be more familiar to physicists.
Directly evaluating the Leibniz formula from the definition requires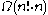
operations in general—that is, a number of operations asymptotically proportional to n factorial
—because n! is the number of order-n permutations. This is impractically difficult for large n. Instead, the determinant can be evaluated in O(n3) operations by forming the LU decomposition
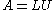(typically via Gaussian elimination
or similar methods), in which case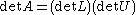
and the determinants of the triangular matrices L and U are simply the products of their diagonal entries. (In practical applications of numerical linear algebra, however, explicit computation of the determinant is rarely required.) See, for example, Trefethen and Bau (1997).
There exists exactly one function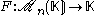
which is alternate
multilinear w.r.t. columns and such that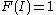
.
Proof.
Uniqueness: Let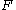
be such a function, and let 
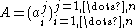be an 
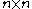matrix. Call 
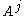the 
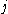-th column of 
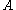, i.e. 
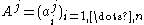, so that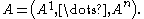 
Also, let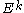
denote the 
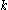-th column vector of the identity matrix.
Now one writes each of the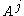
's in terms of the 
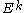, i.e.
.
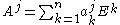As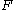
is multilinear, one has
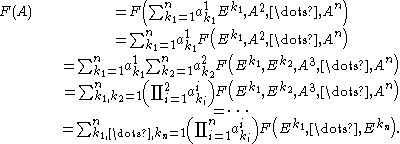
From alternation, it follows that if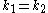
then
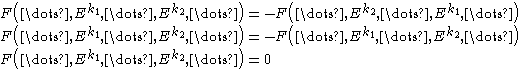
As the above sum takes into account all the possible choices of ordered
-tuples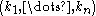 
, and because 
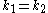implies that F is zero, the sum can be reduced from all tuples to permutations as
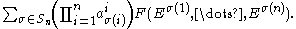
Because F is alternating, the columns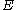
can be swapped until it becomes the identity. The sign function
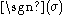is defined to count the number of swaps necessary and account for the resulting sign change. One finally gets:
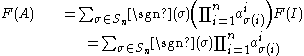
as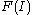
is required to be equal to 
.
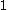Therefore no function besides the function defined by the Leibniz Formula is a multilinear alternating function with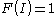
.
Existence: We now show that F, where F is the function defined by the Leibniz formula, has these three properties.
Multilinear: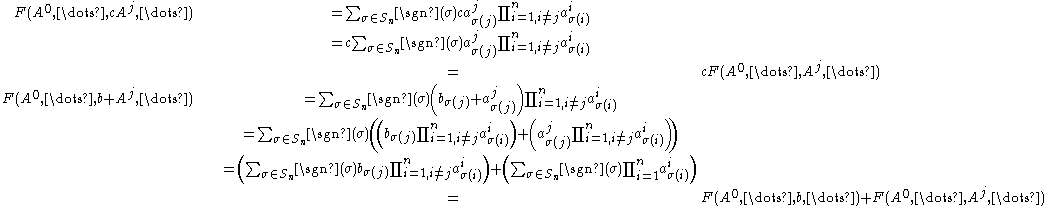
Alternating
:
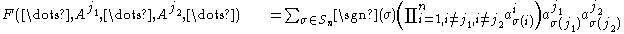
Now let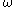
be the tuple equal to 
with the 
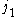and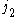 
indices switched. It follows from the definition of 
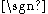that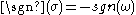 
.
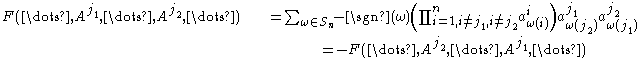
Finally,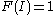
:
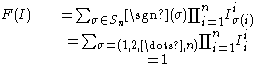
Thus the only functions which are multilinear alternating with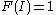
are restricted to the function defined by the Leibniz formula, and it in fact also has these three properties. Hence the determinant can be defined as the only function
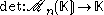
with these three properties.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the Leibniz formula expresses the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a square matrix
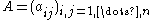
in terms of permutations of the matrix elements. Named in honor of Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, the formula is
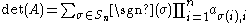
for an n×n matrix, where sgn is the sign function
Even and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
of permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s in the permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
Sn, which returns +1 and −1 for even and odd permutations
Even and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
, respectively.
Another common notation used for the formula is in terms of the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
and makes use of the Einstein summation notation, where it becomes
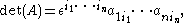
which may be more familiar to physicists.
Directly evaluating the Leibniz formula from the definition requires
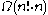operations in general—that is, a number of operations asymptotically proportional to n factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
—because n! is the number of order-n permutations. This is impractically difficult for large n. Instead, the determinant can be evaluated in O(n3) operations by forming the LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
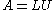(typically via Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
or similar methods), in which case
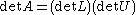and the determinants of the triangular matrices L and U are simply the products of their diagonal entries. (In practical applications of numerical linear algebra, however, explicit computation of the determinant is rarely required.) See, for example, Trefethen and Bau (1997).Formal statement and proof
Theorem.There exists exactly one function
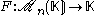
which is alternate
Alternatization
In mathematics, the notion of alternatization or alternatisation is used to pass from any map to an alternating map.Let S be a set and A an Abelian group...
multilinear w.r.t. columns and such that
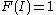.Proof.
Uniqueness: Let
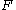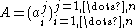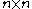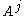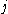be such a function, and let be an matrix. Call the -th column of 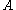, i.e. 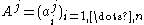, so that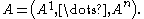 Also, let
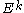denote the 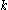-th column vector of the identity matrix.Now one writes each of the
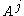's in terms of the 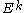, i.e.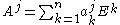.As
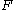is multilinear, one has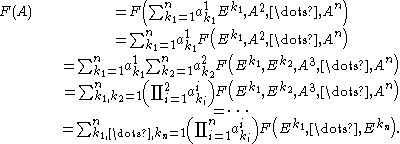From alternation, it follows that if
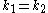then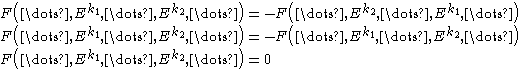As the above sum takes into account all the possible choices of ordered
-tuples 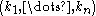, and because 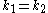implies that F is zero, the sum can be reduced from all tuples to permutations as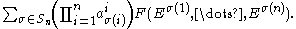Because F is alternating, the columns
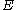can be swapped until it becomes the identity. The sign functionEven and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
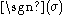is defined to count the number of swaps necessary and account for the resulting sign change. One finally gets: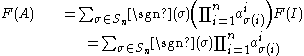as
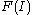is required to be equal to 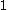.Therefore no function besides the function defined by the Leibniz Formula is a multilinear alternating function with
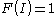.Existence: We now show that F, where F is the function defined by the Leibniz formula, has these three properties.
Multilinear:
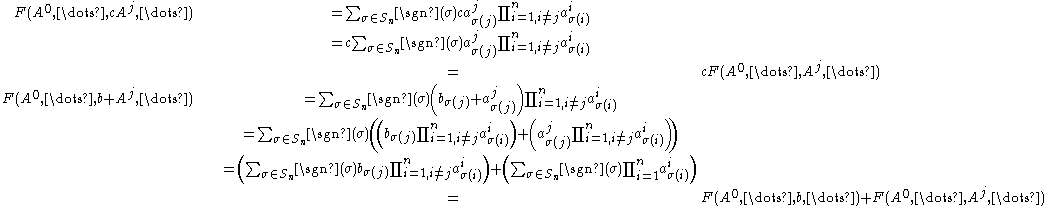
Alternating
Alternating
Alternating may refer to:In mathematics:*alternating form*alternating group*alternating series*alternating knot*alternating mapIn electronics:*alternating current...
:
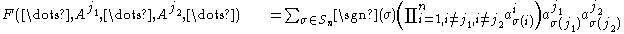
Now let
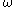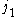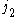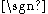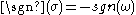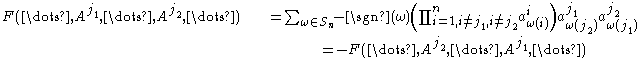
be the tuple equal to with the and indices switched. It follows from the definition of that .Finally,
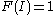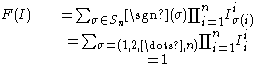
:Thus the only functions which are multilinear alternating with
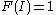are restricted to the function defined by the Leibniz formula, and it in fact also has these three properties. Hence the determinant can be defined as the only function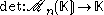with these three properties.