Le Cam's theorem
Encyclopedia
In probability theory
, Le Cam's theorem, named after Lucien le Cam
(1924 – 2000), is as follows.
Suppose:
Then
In other words, the sum has approximately a Poisson distribution
.
By setting pi = 2λn2/n, we see that this generalizes the usual Poisson limit theorem
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Le Cam's theorem, named after Lucien le Cam
Lucien le Cam
Lucien Marie Le Cam was a mathematician and statistician. He obtained a Ph.D. in 1952 at the University of California, Berkeley, was appointed Assistant Professor in 1953 and continued working there beyond his retirement in 1991 until his death.Le Cam was the major figure during the period 1950...
(1924 – 2000), is as follows.
Suppose:
- X1, ..., Xn are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, each with a Bernoulli distribution (i.e., equal to either 0 or 1), not necessarily identically distributed.
- Pr(Xi = 1) = pi for i = 1, 2, 3, ...
-
(i.e.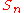 
follows a Poisson binomial distribution)
Then
In other words, the sum has approximately a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
.
By setting pi = 2λn2/n, we see that this generalizes the usual Poisson limit theorem
Poisson limit theorem
The Poisson theorem gives a Poisson approximation to the binomial distribution, under certain conditions. The theorem was named after Siméon-Denis Poisson .- The theorem :If...
.