
Poisson limit theorem
Encyclopedia
The Poisson theorem gives a Poisson
approximation to the binomial distribution, under certain conditions. The theorem was named after Siméon-Denis Poisson (1781–1840).
 , such that
, such that 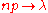
then
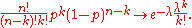
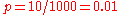 . Here
. Here  so that
so that  . The probabilistically precise way of describing the number of points in the sub-interval would be to describe it as a binomial distribution
. The probabilistically precise way of describing the number of points in the sub-interval would be to describe it as a binomial distribution  . That is, the probability that
. That is, the probability that 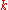 points lie in the sub-interval is
points lie in the sub-interval is

But using the Poisson Theorem we can approximate it as

's rate of growth
, we replace factorials of large numbers with approximations:
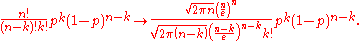
After simplifying the fraction: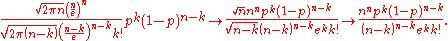
After using the condition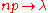 :
: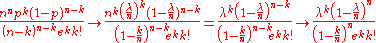
Apply, that due to we get
we get 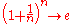 :
:
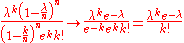
Q.E.D.
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
approximation to the binomial distribution, under certain conditions. The theorem was named after Siméon-Denis Poisson (1781–1840).
The theorem
If , such that
, such that 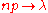
then
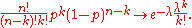
Example
Suppose that in an interval of length 1000, 500 points are placed randomly. Now what is the number points that will be placed in a sub-interval of length 10? If we look here, the probability that a random point will be placed in the sub-interval is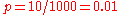 . Here
. Here  so that
so that  . The probabilistically precise way of describing the number of points in the sub-interval would be to describe it as a binomial distribution
. The probabilistically precise way of describing the number of points in the sub-interval would be to describe it as a binomial distribution  . That is, the probability that
. That is, the probability that 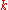 points lie in the sub-interval is
points lie in the sub-interval is
But using the Poisson Theorem we can approximate it as

The proof
Accordingly to factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
's rate of growth
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
, we replace factorials of large numbers with approximations:
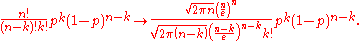
After simplifying the fraction:
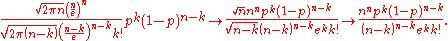
After using the condition
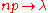 :
: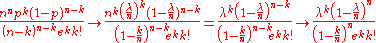
Apply, that due to
 we get
we get 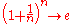 :
: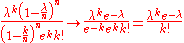
Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...

