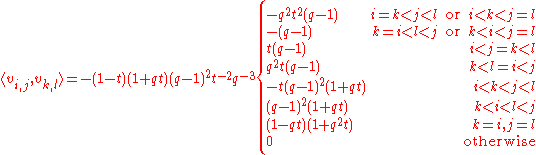Lawrence–Krammer representation
Encyclopedia
In mathematics
the Lawrence–Krammer representation is a representation
of the braid group
s. It fits into a family of representations called the Lawrence representations. The 1st Lawrence representation is the Burau representation
and the 2nd is the Lawrence–Krammer representation.
The Lawrence–Krammer representation is named after Ruth Lawrence
and Daan Krammer.
 to be the mapping class group
to be the mapping class group
of a disc with n marked points . The Lawrence–Krammer representation is defined as the action of
. The Lawrence–Krammer representation is defined as the action of  on the homology of a certain covering
on the homology of a certain covering
space of the configuration space
 . Specifically,
. Specifically, 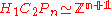 , and the subspace of
, and the subspace of 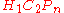 invariant under the action of
invariant under the action of  is primitive, free and of rank 2. Generators for this invariant subspace are denoted by
is primitive, free and of rank 2. Generators for this invariant subspace are denoted by 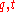 .
.
The covering space of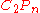 corresponding to the kernel of the projection map
corresponding to the kernel of the projection map
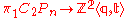
is called the Lawrence–Krammer cover and is denoted . Diffeomorphism
. Diffeomorphism
s of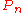 act on
act on 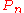 , thus also on
, thus also on 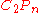 , moreover they lift uniquely to diffeomorphisms of
, moreover they lift uniquely to diffeomorphisms of 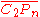 which restrict to identity on the co-dimension two boundary stratum (where both points are on the boundary circle). The action of
which restrict to identity on the co-dimension two boundary stratum (where both points are on the boundary circle). The action of  on
on
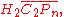
thought of as a
 -module,
-module,
is the Lawrence–Krammer representation. is known to be a free
is known to be a free  -module, of rank
-module, of rank 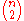 .
.
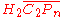 are denoted
are denoted 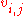 for
for  . Letting
. Letting  denote the standard Artin generators of the braid group
denote the standard Artin generators of the braid group
, we get the expression:
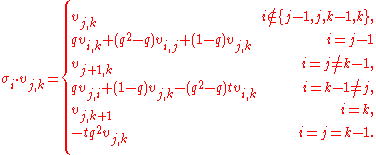
.
which is known to be negative-definite Hermitian provided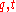 are specialized to suitable unit complex numbers (q near 1 and t near i). Thus the braid group is a subgroup of the unitary group
are specialized to suitable unit complex numbers (q near 1 and t near i). Thus the braid group is a subgroup of the unitary group
of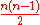 -square matrices. Recently it has been shown that the image of the Lawrence–Krammer representation is dense subgroup
-square matrices. Recently it has been shown that the image of the Lawrence–Krammer representation is dense subgroup
of the unitary group
in this case.
The sesquilinear form has the explicit description:
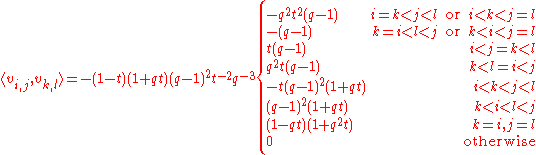
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Lawrence–Krammer representation is a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s. It fits into a family of representations called the Lawrence representations. The 1st Lawrence representation is the Burau representation
Burau representation
In mathematics the Burau representation is a representation of the braid groups, named after and originally studied by the German mathematician Werner Burau during the 1930s...
and the 2nd is the Lawrence–Krammer representation.
The Lawrence–Krammer representation is named after Ruth Lawrence
Ruth Lawrence
Ruth Elke Lawrence-Naimark is an Associate Professor of mathematics at the Einstein Institute of Mathematics, Hebrew University of Jerusalem, and a researcher in knot theory and algebraic topology. Outside academia, she is best known for being a child prodigy in mathematics.- Youth :Ruth Lawrence...
and Daan Krammer.
Definition
Consider the braid groupBraid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
 to be the mapping class group
to be the mapping class groupMapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of a disc with n marked points
 . The Lawrence–Krammer representation is defined as the action of
. The Lawrence–Krammer representation is defined as the action of  on the homology of a certain covering
on the homology of a certain coveringCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
space of the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
 . Specifically,
. Specifically, 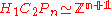 , and the subspace of
, and the subspace of 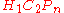 invariant under the action of
invariant under the action of  is primitive, free and of rank 2. Generators for this invariant subspace are denoted by
is primitive, free and of rank 2. Generators for this invariant subspace are denoted by 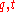 .
.The covering space of
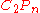 corresponding to the kernel of the projection map
corresponding to the kernel of the projection map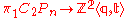
is called the Lawrence–Krammer cover and is denoted
 . Diffeomorphism
. DiffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of
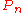 act on
act on 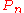 , thus also on
, thus also on 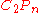 , moreover they lift uniquely to diffeomorphisms of
, moreover they lift uniquely to diffeomorphisms of 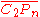 which restrict to identity on the co-dimension two boundary stratum (where both points are on the boundary circle). The action of
which restrict to identity on the co-dimension two boundary stratum (where both points are on the boundary circle). The action of  on
on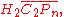
thought of as a
 -module,
-module,is the Lawrence–Krammer representation.
 is known to be a free
is known to be a free  -module, of rank
-module, of rank 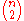 .
.Matrices
Using Bigelow's conventions for the Lawrence–Krammer representation, generators for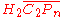 are denoted
are denoted 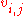 for
for  . Letting
. Letting  denote the standard Artin generators of the braid group
denote the standard Artin generators of the braid groupBraid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
, we get the expression:
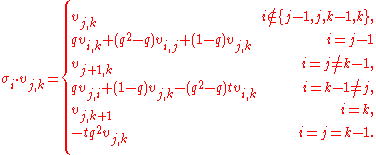
Faithfulness
Stephen Bigelow and Daan Krammer have independent proofs that the Lawrence–Krammer representation is faithfulGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
.
Geometry
The Lawrence–Krammer representation preserves a non-degenerate sesquilinear formSesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
which is known to be negative-definite Hermitian provided
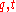 are specialized to suitable unit complex numbers (q near 1 and t near i). Thus the braid group is a subgroup of the unitary group
are specialized to suitable unit complex numbers (q near 1 and t near i). Thus the braid group is a subgroup of the unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
of
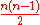 -square matrices. Recently it has been shown that the image of the Lawrence–Krammer representation is dense subgroup
-square matrices. Recently it has been shown that the image of the Lawrence–Krammer representation is dense subgroupDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
of the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
in this case.
The sesquilinear form has the explicit description: