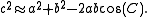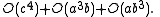.gif)
Law of cosines (spherical)
Encyclopedia
In spherical trigonometry
, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, analogous to the ordinary law of cosines
from plane trigonometry
.
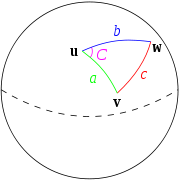Given a unit sphere, a "spherical triangle" on the surface of the sphere is defined by the great circle
s connecting three points u, v, and w on the sphere (shown at right). If the lengths of these three sides are a (from u to v), b (from u to w), and c (from v to w), and the angle of the corner opposite c is C, then the (first) spherical law of cosines states:
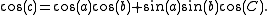
Since this is a unit sphere, the lengths a, b, and c are simply equal to the angles (in radian
s) subtended by those sides from the center of the sphere (for a non-unit sphere, they are the distances divided by the radius). As a special case, for
, then 
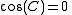and one obtains the spherical analogue of the Pythagorean theorem
:
A variation on the law of cosines, the second spherical law of cosines, (also called the cosine rule for angles) states:
where A and B are the angles of the corners opposite to sides a and b, respectively. It can be obtained from consideration of a spherical triangle dual to the given one.
If the law of cosines is used to solve for c, the necessity of inverting the cosine magnifies rounding errors when c is small. In this case, the alternative formulation of the law of haversines is preferable.
For small spherical triangles, i.e. for small a, b, and c, the spherical law of cosines is approximately the same as the ordinary planar law of cosines,
The error in this approximation, which can be obtained from the Maclaurin series for the cosine and sine functions, is of order
s:
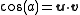
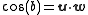
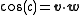
To get the angle C, we need the tangent
vectors ta and tb at u along the directions of sides a and b, respectively. For example, the tangent vector ta is the unit vector perpendicular
to u in the u-v plane, whose direction is given by the component of v perpendicular to u. This means:
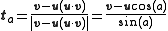
where for the denominator we have used the Pythagorean identity
sin2(a) = 1 − cos2(a). Similarly,
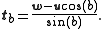
Then, the angle C is given by:
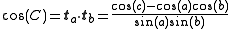
from which the law of cosines immediately follows.
for plane triangles (and remembering that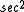
of any angle is 
),
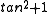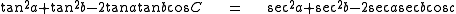
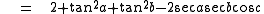
So
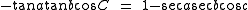
Multiply both sides by
and rearrange.
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, analogous to the ordinary law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
from plane trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
.
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s connecting three points u, v, and w on the sphere (shown at right). If the lengths of these three sides are a (from u to v), b (from u to w), and c (from v to w), and the angle of the corner opposite c is C, then the (first) spherical law of cosines states:
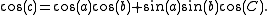
Since this is a unit sphere, the lengths a, b, and c are simply equal to the angles (in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s) subtended by those sides from the center of the sphere (for a non-unit sphere, they are the distances divided by the radius). As a special case, for
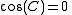, then and one obtains the spherical analogue of the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
:
A variation on the law of cosines, the second spherical law of cosines, (also called the cosine rule for angles) states:
where A and B are the angles of the corners opposite to sides a and b, respectively. It can be obtained from consideration of a spherical triangle dual to the given one.
If the law of cosines is used to solve for c, the necessity of inverting the cosine magnifies rounding errors when c is small. In this case, the alternative formulation of the law of haversines is preferable.
For small spherical triangles, i.e. for small a, b, and c, the spherical law of cosines is approximately the same as the ordinary planar law of cosines,
The error in this approximation, which can be obtained from the Maclaurin series for the cosine and sine functions, is of order
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
Proof
A proof of the law of cosines can be constructed as follows. Let u, v, and w denote the unit vectors from the center of the sphere to those corners of the triangle. Then, the lengths (angles) of the sides are given by the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s:
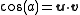
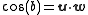
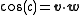
To get the angle C, we need the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
vectors ta and tb at u along the directions of sides a and b, respectively. For example, the tangent vector ta is the unit vector perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to u in the u-v plane, whose direction is given by the component of v perpendicular to u. This means:
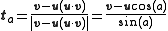
where for the denominator we have used the Pythagorean identity
Pythagorean trigonometric identity
The Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
sin2(a) = 1 − cos2(a). Similarly,
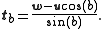
Then, the angle C is given by:
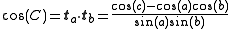
from which the law of cosines immediately follows.
Proof without vectors
To the diagram above, add a plane tangent to the sphere at u, and extend radii from the center of the sphere O to meet the plane at points y and z. We then have two plane triangles with a side in common: the triangle containing u, y and z and the one containing O, y and z. Sides of the first triangle are tan a and tan b, with angle C between them; sides of the second triangle are sec a and sec b, with angle c between them. By the law of cosinesLaw of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
for plane triangles (and remembering that
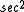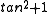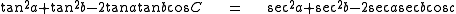
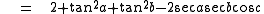
of any angle is ),So
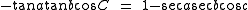
Multiply both sides by
and rearrange.