
Largest remainder method
Encyclopedia
The largest remainder method (also known as Hare-Niemeyer method or as Vinton's method ) is one way of allocating seats proportionally
for representative assemblies with party list
voting systems. It contrasts with the highest averages method
.
part plus a fractional
remainder
. Each party is first allocated a number of seats equal to their integer. This will generally leave some seats unallocated: the parties are then ranked on the basis of the fractional remainders, and the parties with the largest remainders are each allocated one additional seat until all the seats have been allocated. This gives the method its name.
the Hare quota
and the Droop quota
.
The Hare (or simple) Quota is defined as follows
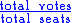
The Hamilton method of apportionment is actually a largest-remainder method which uses the Hare Quota. It is named after Alexander Hamilton
, who invented the largest-remainder method in 1792. It is used for legislative elections in Russia
(with a 7% exclusion threshold since 2007), Ukraine
(3% threshold), Namibia
and the territory of Hong Kong
. It was historically applied for congressional apportionment
in the United States
during the 19th century.
The Droop quota
is the integer part of
and is applied in elections in South Africa. The Hagenbach-Bischoff quota
is virtually identical, being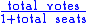
either used as a fraction or rounded up.
The Hare quota tends to be slightly more generous to less popular parties and the Droop quota to more popular parties, and can arguably be considered more proportional than Droop quota although it is more likely to give fewer than half the seats to a list with more than half the vote.
The Imperiali quota
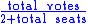
is rarely used since it suffers from the defect that it might result in more seats being allocated than there are available (this can also occur with the Hagenbach-Bischoff quota
but it is very unlikely, and it is impossible with the Hare and Droop quotas). This will certainly happen if there are only two parties. In such a case, it is usual to increase the quota until the number of candidates elected is equal to the number of seats available, in effect changing the voting system to the Jefferson apportionment formula (see D'Hondt method
).
. The Alabama paradox is exhibited when an increase in seats apportioned leads to a decrease in the number of seats allocated to a certain party. Suppose 25 seats are to be apportioned between 6 parties with votes cast in the proportions 1500:1500:900:500:500:200. The two parties with 500 votes get three seats each. Now allocate 26 seats, and it will be found that the these parties get only two seats apiece.
With 25 seats, we get:
With 26 seats, we have:
Apportionment (politics)
Apportionment is the process of allocating political power among a set of principles . In most representative governments, political power has most recently been apportioned among constituencies based on population, but there is a long history of different approaches.The United States Constitution,...
for representative assemblies with party list
Party-list proportional representation
Party-list proportional representation systems are a family of voting systems emphasizing proportional representation in elections in which multiple candidates are elected...
voting systems. It contrasts with the highest averages method
Highest averages method
The highest averages method is the name for a variety of ways to allocate seats proportionally for representative assemblies with party list voting systems....
.
Method
The largest remainder method requires the numbers of votes for each party to be divided by a quota representing the number of votes required for a seat (i.e. usually the total number of votes cast divided by the number of seats, or some similar formula). The result for each party will usually consist of an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
part plus a fractional
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
. Each party is first allocated a number of seats equal to their integer. This will generally leave some seats unallocated: the parties are then ranked on the basis of the fractional remainders, and the parties with the largest remainders are each allocated one additional seat until all the seats have been allocated. This gives the method its name.
Quotas
There are several possibilities for the quota. The most common are:the Hare quota
Hare quota
The Hare quota is a formula used under some forms of the Single Transferable Vote system and the largest remainder method of party-list proportional representation...
and the Droop quota
Droop Quota
The Droop quota is the quota most commonly used in elections held under the Single Transferable Vote system. It is also sometimes used in elections held under the largest remainder method of party-list proportional representation . In an STV election the quota is the minimum number of votes a...
.
The Hare (or simple) Quota is defined as follows
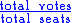
The Hamilton method of apportionment is actually a largest-remainder method which uses the Hare Quota. It is named after Alexander Hamilton
Alexander Hamilton
Alexander Hamilton was a Founding Father, soldier, economist, political philosopher, one of America's first constitutional lawyers and the first United States Secretary of the Treasury...
, who invented the largest-remainder method in 1792. It is used for legislative elections in Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
(with a 7% exclusion threshold since 2007), Ukraine
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
(3% threshold), Namibia
Namibia
Namibia, officially the Republic of Namibia , is a country in southern Africa whose western border is the Atlantic Ocean. It shares land borders with Angola and Zambia to the north, Botswana to the east and South Africa to the south and east. It gained independence from South Africa on 21 March...
and the territory of Hong Kong
Legislative Council of Hong Kong
The Legislative Council is the unicameral legislature of Hong Kong.-History:The Legislative Council of Hong Kong was set up in 1843 as a colonial legislature under British rule...
. It was historically applied for congressional apportionment
United States congressional apportionment
United States congressional apportionment is the process by which seats in the United States House of Representatives are redistributed amongst the 50 states following each constitutionally mandated decennial census. Each state is apportioned a number of seats which approximately corresponds to its...
in the United States
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
during the 19th century.
The Droop quota
Droop Quota
The Droop quota is the quota most commonly used in elections held under the Single Transferable Vote system. It is also sometimes used in elections held under the largest remainder method of party-list proportional representation . In an STV election the quota is the minimum number of votes a...
is the integer part of

and is applied in elections in South Africa. The Hagenbach-Bischoff quota
Hagenbach-Bischoff quota
The Hagenbach-Bischoff quota is a formula used in some voting systems based on proportional representation . It is used in some elections held under the largest remainder method of party-list proportional representation as well as in a variant of the D'Hondt method known as the Hagenbach-Bischoff...
is virtually identical, being
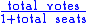
either used as a fraction or rounded up.
The Hare quota tends to be slightly more generous to less popular parties and the Droop quota to more popular parties, and can arguably be considered more proportional than Droop quota although it is more likely to give fewer than half the seats to a list with more than half the vote.
The Imperiali quota
Imperiali quota
The Imperiali quota is a formula used to calculate the minimum number, or quota, of votes required to capture a seat in some forms of single transferable vote or largest remainder method party-list proportional representation voting systems....
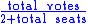
is rarely used since it suffers from the defect that it might result in more seats being allocated than there are available (this can also occur with the Hagenbach-Bischoff quota
Hagenbach-Bischoff quota
The Hagenbach-Bischoff quota is a formula used in some voting systems based on proportional representation . It is used in some elections held under the largest remainder method of party-list proportional representation as well as in a variant of the D'Hondt method known as the Hagenbach-Bischoff...
but it is very unlikely, and it is impossible with the Hare and Droop quotas). This will certainly happen if there are only two parties. In such a case, it is usual to increase the quota until the number of candidates elected is equal to the number of seats available, in effect changing the voting system to the Jefferson apportionment formula (see D'Hondt method
D'Hondt method
The d'Hondt method is a highest averages method for allocating seats in party-list proportional representation. The method described is named after Belgian mathematician Victor D'Hondt who described it in 1878...
).
Hare quota
| Party | Yellows | Whites | Reds | Greens | Blues | Pinks | Total |
| Votes | 47,000 | 16,000 | 15,800 | 12,000 | 6,100 | 3,100 | 100,000 |
| Seats | 10 | ||||||
| Hare Quota | 10,000 | ||||||
| Votes/Quota | 4.70 | 1.60 | 1.58 | 1.20 | 0.61 | 0.31 | |
| Automatic seats | 4 | 1 | 1 | 1 | 0 | 0 | 7 |
| Remainder | 0.70 | 0.60 | 0.58 | 0.20 | 0.61 | 0.31 | |
| Highest Remainder Seats | 1 | 1 | 0 | 0 | 1 | 0 | 3 |
| Total Seats | 5 | 2 | 1 | 1 | 1 | 0 | 10 |
Droop quota
| Party | Yellows | Whites | Reds | Greens | Blues | Pinks | Total |
| Votes | 47,000 | 16,000 | 15,800 | 12,000 | 6,100 | 3,100 | 100,000 |
| Seats | 10 | ||||||
| Droop Quota | 9,091 | ||||||
| Votes/Quota | 5.170 | 1.760 | 1.738 | 1.320 | 0.671 | 0.341 | |
| Automatic seats | 5 | 1 | 1 | 1 | 0 | 0 | 8 |
| Remainder | 0.170 | 0.760 | 0.738 | 0.320 | 0.671 | 0.341 | |
| Highest Remainder Seats | 0 | 1 | 1 | 0 | 0 | 0 | 2 |
| Total Seats | 5 | 2 | 2 | 1 | 0 | 0 | 10 |
Pros and cons
- It is relatively easy for a voter to understand how the largest remainder method allocates seats. If the Hare quota is used, the method gives no advantage to lists with either a large or a small proportion of the votes—to that extent it is neutral. However, whether a list gets an extra seat or not may well depend on how the remaining votes are distributed among other parties: it is quite possible for a party to make a slight percentage gain yet lose a seat if the votes for other parties also change. A related feature is that increasing the number of seats may cause a party to lose a seat (the so-called Alabama paradox). The highest averages methodHighest averages methodThe highest averages method is the name for a variety of ways to allocate seats proportionally for representative assemblies with party list voting systems....
s avoid these paradoxes.
Technical evaluation and paradoxes
The largest remainder method is the only apportionment that satisfies the quota rule; in fact, it is designed to satisfy this criterion. However, it comes at the cost of paradoxical behaviourApportionment paradox
An apportionment paradox exists when the rules for apportionment in a political system produce results which are unexpected or seem to violate common sense.To apportion is to divide into parts according to some rule, the rule typically being one of proportion...
. The Alabama paradox is exhibited when an increase in seats apportioned leads to a decrease in the number of seats allocated to a certain party. Suppose 25 seats are to be apportioned between 6 parties with votes cast in the proportions 1500:1500:900:500:500:200. The two parties with 500 votes get three seats each. Now allocate 26 seats, and it will be found that the these parties get only two seats apiece.
With 25 seats, we get:
| Party | A | B | C | D | E | F | Total |
| Votes | 1500 | 1500 | 900 | 500 | 500 | 200 | 5100 |
| Seats | 25 | ||||||
| Hare Quota | 204 | ||||||
| Quotas Received | 7.35 | 7.35 | 4.41 | 2.45 | 2.45 | 0.98 | |
| Automatic seats | 7 | 7 | 4 | 2 | 2 | 0 | 22 |
| Remainder | 0.35 | 0.35 | 0.41 | 0.45 | 0.45 | 0.98 | |
| Surplus seats | 0 | 0 | 0 | 1 | 1 | 1 | 3 |
| Total Seats | 7 | 7 | 4 | 3 | 3 | 1 | 25 |
With 26 seats, we have:
| Party | A | B | C | D | E | F | Total |
| Votes | 1500 | 1500 | 900 | 500 | 500 | 200 | 5100 |
| Seats | 26 | ||||||
| Hare Quota | 196 | ||||||
| Quotas Received | 7.65 | 7.65 | 4.59 | 2.55 | 2.55 | 1.02 | |
| Automatic seats | 7 | 7 | 4 | 2 | 2 | 1 | 23 |
| Remainder | 0.65 | 0.65 | 0.59 | 0.55 | 0.55 | 0.02 | |
| Surplus seats | 1 | 1 | 1 | 0 | 0 | 0 | 3 |
| Total Seats | 8 | 8 | 5 | 2 | 2 | 1 | 26 |
External links
- Hamilton method experimentation applet at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

