Highest averages method
Encyclopedia
The highest averages method is the name for a variety of ways to allocate seats proportionally for representative assemblies with party list
voting systems.
An alternative to this method is the largest remainder method
, which uses a minimum quota which can be calculated in a number of ways.
or average, up to the total number of seats available.
, using the divisors 1, 2, 3, 4, etc. This system tends to give larger parties a slightly larger portion of seats than their portion of the electorate, and thus guarantees that a party with a majority of voters will get at least half of the seats.
divides the number of votes for each party by the odd numbers (1, 3, 5, 7 etc.). This system does not inherently favour larger parties over smaller (or vice versa), and may thus be considered "more proportional" than d'Hondt.
- Alternatively, dividing the votes numbers by 0.5, 1.5, 2.5, 3.5 etc. yields the same result.
The Sainte-Laguë method is sometimes modified by increasing the first divisor to e.g. 1.4, to discourage very small parties gaining their first seat "too cheaply".
which is a Largest remainder method
). The divisors are 2,3,4 etc. It is designed to disfavor the smallest parties, akin to a "cutoff", and is used only in Belgian municipal elections
.
, the divisors are given by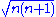
, which makes sense only if every party is guaranteed at least one seat: this is used for allotting seats in the US House of Representatives
to the states. (This is not an election, of course.)
). Parties are then allocated seats by determining how many quotas they have won, by dividing their vote totals by the quota. Where a party wins a fraction of a quota, this can be rounded down or rounded to the nearest whole number. Rounding down is equivalent to using the d'Hondt method, while rounding to the nearest whole number is equivalent to the Sainte-Laguë method. However, because of the rounding, this will not necessarily result in the desired number of seats being filled. In that case, the quota may be adjusted up or down until the number of seats after rounding is equal to the desired number.
The tables used in the d'Hondt or Sainte-Laguë methods can then be viewed as calculating the highest quota possible to round off to a given number of seats. For example, the quotient which wins the first seat in a d'Hondt calculation is the highest quota possible to have one party's vote, when rounded down, be greater than 1 quota and thus allocate 1 seat. The quotient for the second round is the highest divisor possible to have a total of 2 seats allocated, and so on.
d'Hondt method Sainte-Laguë method (unmodified)
party
Yellow White Red Green Blue Pink
Yellow White Red Green Blue Pink
votes
47,000 16,000 15,900 12,000 6,000 3,100
47,000 16,000 15,900 12,000 6,000 3,100
mandate quotient
1
47,000
16,000
15,900
12,000
6,000
3,100
47,000
16,000
15,900
12,000
6,000
3,100
2
23,500
8,000
7,950
6,000
3,000
1,550
15,667
5,333
5,300
4,000
2,000
1,033
3
15,667
5,333
5,300
4,000
2,000
1,033
9,400
3,200
3,180
2,400
1,200
620
4
11,750
4,000
3,975
3,000
1,500
775
6,714
2,857
2,271
1,714
875
443
5
9,400
3,200
3,180
2,400
1,200
620
5,222
1,778
1,767
1,333
667
333
6
7,833
2,667
2,650
2,000
1,000
517
4,273
1,454
1,445
1,091
545
282
seat
seat allocation
1
47,000
47,000
2
23,500
16,000
3
16,000
15,900
4
15,900
15,667
5
15,667
12,000
6
12,000
9,400
7
11,750
6,714
8
9,400
6,000
9
8,000
5,333
10
7,950
5,300
With the modification, the methods are initially more similar:
d'Hondt method modified Sainte-Laguë method
parties
Yellows Whites Reds Greens Blues Pinks
Yellows Whites Reds Greens Blues Pinks
votes
47,000 16,000 15,900 12,000 6,000 3,100
47,000 16,000 15,900 12,000 6,000 3,100
mandate quotient
1
47,000
16,000
15,900
12,000
6,000
3,100
33,571
11,429
11,357
8,571
4,286
2,214
2
23,500
8,000
7,950
6,000
3,000
1,550
15,667
5,333
5,300
4,000
2,000
1,033
3
15,667
5,333
5,300
4,000
2,000
1,033
9,400
3,200
3,180
2,400
1,200
620
4
11,750
4,000
3,975
3,000
1,500
775
6,714
2,857
2,271
1,714
875
443
5
9,400
3,200
3,180
2,400
1,200
620
5,222
1,778
1,767
1,333
667
333
6
7,833
2,667
2,650
2,000
1,000
517
4,273
1,454
1,445
1,091
545
282
seat
seat allocation
1
47,000
33,571
2
23,500
15,667
3
16,000
11,429
4
15,900
11,357
5
15,667
9,400
6
12,000
8,571
7
11,750
6,714
8
9,400
5,333
9
8,000
5,300
10
7,950
5,222
Party-list proportional representation
Party-list proportional representation systems are a family of voting systems emphasizing proportional representation in elections in which multiple candidates are elected...
voting systems.
An alternative to this method is the largest remainder method
Largest remainder method
The largest remainder method is one way of allocating seats proportionally for representative assemblies with party list voting systems...
, which uses a minimum quota which can be calculated in a number of ways.
Individual methods
The highest averages method requires the number of votes for each party to be divided successively by a series of divisors, and seats are allocated to parties that secure the highest resulting quotientQuotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
or average, up to the total number of seats available.
d'Hondt method
The most widely used is the d'Hondt formulaD'Hondt method
The d'Hondt method is a highest averages method for allocating seats in party-list proportional representation. The method described is named after Belgian mathematician Victor D'Hondt who described it in 1878...
, using the divisors 1, 2, 3, 4, etc. This system tends to give larger parties a slightly larger portion of seats than their portion of the electorate, and thus guarantees that a party with a majority of voters will get at least half of the seats.
Sainte-Laguë method
The Sainte-Laguë methodSainte-Laguë method
The Sainte-Laguë method is one way of allocating seats approximately proportional to the number of votes of a party to a party list used in many voting systems. It is named after the French mathematician André Sainte-Laguë. The Sainte-Laguë method is quite similar to the D'Hondt method, but uses...
divides the number of votes for each party by the odd numbers (1, 3, 5, 7 etc.). This system does not inherently favour larger parties over smaller (or vice versa), and may thus be considered "more proportional" than d'Hondt.
- Alternatively, dividing the votes numbers by 0.5, 1.5, 2.5, 3.5 etc. yields the same result.
The Sainte-Laguë method is sometimes modified by increasing the first divisor to e.g. 1.4, to discourage very small parties gaining their first seat "too cheaply".
Imperiali
Another highest average method is called Imperiali (not to be confused with the Imperiali quotaImperiali quota
The Imperiali quota is a formula used to calculate the minimum number, or quota, of votes required to capture a seat in some forms of single transferable vote or largest remainder method party-list proportional representation voting systems....
which is a Largest remainder method
Largest remainder method
The largest remainder method is one way of allocating seats proportionally for representative assemblies with party list voting systems...
). The divisors are 2,3,4 etc. It is designed to disfavor the smallest parties, akin to a "cutoff", and is used only in Belgian municipal elections
Belgian municipal elections, 2006
The Belgian provincial and municipal elections, 2006 took place on Sunday 8 October 2006. The electors have elected the municipal counsellors of 589 cities and towns as well as the ten provincial councils...
.
Huntington-Hill method
In the Huntington-Hill methodHuntington-Hill method
The Huntington–Hill method of apportionment assigns seats by finding a modified divisor D such that each constituency's priority quotient , using the geometric mean of the lower and upper quota for the divisor, yields the correct number of seats that minimizes the percentage differences in the size...
, the divisors are given by
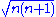, which makes sense only if every party is guaranteed at least one seat: this is used for allotting seats in the US House of RepresentativesUnited States congressional apportionment
United States congressional apportionment is the process by which seats in the United States House of Representatives are redistributed amongst the 50 states following each constitutionally mandated decennial census. Each state is apportioned a number of seats which approximately corresponds to its...
to the states. (This is not an election, of course.)
Quota system
In addition to the procedure above, highest averages methods can be conceived of in a different way. For an election, a quota is calculated, usually the total number of votes cast divided by the number of seats to be allocated (the Hare quotaHare quota
The Hare quota is a formula used under some forms of the Single Transferable Vote system and the largest remainder method of party-list proportional representation...
). Parties are then allocated seats by determining how many quotas they have won, by dividing their vote totals by the quota. Where a party wins a fraction of a quota, this can be rounded down or rounded to the nearest whole number. Rounding down is equivalent to using the d'Hondt method, while rounding to the nearest whole number is equivalent to the Sainte-Laguë method. However, because of the rounding, this will not necessarily result in the desired number of seats being filled. In that case, the quota may be adjusted up or down until the number of seats after rounding is equal to the desired number.
The tables used in the d'Hondt or Sainte-Laguë methods can then be viewed as calculating the highest quota possible to round off to a given number of seats. For example, the quotient which wins the first seat in a d'Hondt calculation is the highest quota possible to have one party's vote, when rounded down, be greater than 1 quota and thus allocate 1 seat. The quotient for the second round is the highest divisor possible to have a total of 2 seats allocated, and so on.
Comparison between the d'Hondt and Sainte-Laguë methods
D'Hondt and Sainte-Laguë allow different strategies by parties looking to maximize their seat allocation. D'Hondt favors the merging of parties, while Sainte-Laguë favours neither merging nor splitting parties which expect to gain more than 1 or 2 seats. (It does favor splitting of very small parties (expecting to gain only 1-2 seats) into still smaller ones). Modified Saint-Laguë prevents this splitting advantage for small parties, while remaining impartial towards party size for all larger parties.Examples
With the modification, the methods are initially more similar: