Landau's problems
Encyclopedia
At the 1912 International Congress of Mathematicians
, Edmund Landau
listed four basic problems about primes
. These problems were characterised in his speech as "unattackable at the present state of science" and are now known as Landau's problems. They are as follows:
, all four problems are unresolved.
proves Goldbach's weak conjecture
for sufficiently large n. Deshouillers, Effinger, te Riele and Zinoviev conditionally proved the weak conjecture under the GRH
. The weak conjecture is known to hold for all n outside the range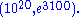
Chen's theorem
proves that for all sufficiently large n,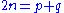
where p is prime and q is either prime or semiprime
. Montgomery and Vaughan showed that the exceptional set (even numbers not expressible as the sum of two primes) was of density
zero.
, Pintz
and Yıldırım
showed that the size of the gap between primes could be far smaller than the average size of the prime gap: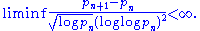
Earlier, they conditionally proved a weaker version of the twin prime conjecture, that infinitely many primes p exist with
, under the Elliott–Halberstam conjecture. 
is the prime-counting function. The twin prime conjecture replaces 20 with 2.
Chen
showed that there are infinitely many primes p (later called Chen prime
s) such that p+2 is either a prime or a semiprime.
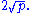A table of maximal prime gaps shows that the conjecture holds to 1018. A counterexample near 1018 would require a prime gap fifty million times the size of the average gap.
A result due to Ingham
shows that there is a prime between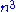
and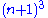 
for every large enough n.
.
Iwaniec
showed that there are infinitely many numbers of the form
with at most two prime factors.
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
, Edmund Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
listed four basic problems about primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. These problems were characterised in his speech as "unattackable at the present state of science" and are now known as Landau's problems. They are as follows:
- Goldbach's conjectureGoldbach's conjectureGoldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
: Can every even integer greater than 2 be written as the sum of two primes? - Twin prime conjecture: Are there infinitely many primes p such that p + 2 is prime?
- Legendre's conjectureLegendre's conjectureLegendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
: Does there always exist at least one prime between consecutive perfect squaresSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
? - Are there infinitely many primes p such that p − 1 is a perfect square? In other words: Are there infinitely many primes of the form n2 + 1? .
, all four problems are unresolved.
Goldbach's conjecture
Vinogradov's theoremVinogradov's theorem
In number theory, Vinogradov's theorem implies that any sufficiently large odd integer can be written as a sum of three prime numbers. It is a weaker form of Goldbach's conjecture, which would imply the existence of such a representation for all odd integers greater than five. It is named after...
proves Goldbach's weak conjecture
Goldbach's weak conjecture
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that:...
for sufficiently large n. Deshouillers, Effinger, te Riele and Zinoviev conditionally proved the weak conjecture under the GRH
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
. The weak conjecture is known to hold for all n outside the range
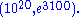
Chen's theorem
Chen's theorem
right|thumb|Chen JingrunChen's theorem states that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime . The theorem was first stated by Chinese mathematician Chen Jingrun in 1966, with further details of the proof in 1973. His original...
proves that for all sufficiently large n,
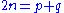where p is prime and q is either prime or semiprimeSemiprime
In mathematics, a semiprime is a natural number that is the product of two prime numbers. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... ....
. Montgomery and Vaughan showed that the exceptional set (even numbers not expressible as the sum of two primes) was of density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
zero.
Twin prime conjecture
GoldstonDaniel Goldston
Daniel Alan Goldston is an American mathematician who specializes in number theory. He is currently a professor of mathematics at San Jose State University....
, Pintz
János Pintz
János Pintz is a Hungarian mathematician working in analytic number theory. He is a fellow of the Rényi Mathematical Institute and is also a member of the Hungarian Academy of Sciences.-Mathematical results:...
and Yıldırım
Cem Yildirim
Cem Yalçın Yıldırım is a Turkish mathematician who specializes in number theory. He obtained his PhD from the University of Toronto in 1990. His advisor was John Friedlander...
showed that the size of the gap between primes could be far smaller than the average size of the prime gap:
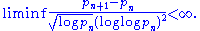
Earlier, they conditionally proved a weaker version of the twin prime conjecture, that infinitely many primes p exist with
, under the Elliott–Halberstam conjecture. 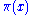is the prime-counting function. The twin prime conjecture replaces 20 with 2.Chen
Chen Jingrun
Chen Jingrun was a Chinese mathematician who made significant contributions to number theory.- Personal life :Chen was the third son in a large family from Fuzhou, Fujian, China. His father was a postal worker. Chen Jingrun graduated from the Mathematics Department of Xiamen University in 1953...
showed that there are infinitely many primes p (later called Chen prime
Chen prime
A prime number p is called a Chen prime if p + 2 is either a prime or a product of two primes. The even number 2p + 2 therefore satisfies Chen's theorem....
s) such that p+2 is either a prime or a semiprime.
Legendre's conjecture
It suffices to check that each prime gap starting at p is smaller than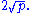 A table of maximal prime gaps shows that the conjecture holds to 1018. A counterexample near 1018 would require a prime gap fifty million times the size of the average gap.A result due to Ingham
Albert Ingham
Albert Edward Ingham was an English mathematician.Ingham was born in Northampton. He went to Stafford Grammar School and Trinity College, Cambridge . He obtained his Ph.D., which was supervised by John Edensor Littlewood, from the University of Cambridge. He supervised the Ph.D.s of C. Brian...
shows that there is a prime between
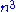and 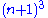for every large enough n.Near-square primes
The Friedlander–Iwaniec theorem shows that infinitely many primes are of the form.Iwaniec
Henryk Iwaniec
Henryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
showed that there are infinitely many numbers of the form
with at most two prime factors.