LOBPCG
Encyclopedia
Locally Optimal Block Preconditioned Conjugate Gradient Method (LOBPCG) is an algorithm, proposed in (Knyazev, 2001), for finding the largest (or smallest) eigenvalues and the corresponding eigenvectors of a symmetric positive definite generalized eigenvalue problem.
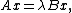
for a given pair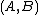
of complex Hermitian or real symmetric matrices, where
the matrix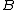
is also assumed positive-definite
.
The method performs an iterative maximization (or minimization) of the generalized Rayleigh quotient
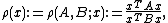
which results in finding largest (or smallest) eigenpairs of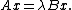
The direction of the steepest accent, which is the gradient
, of the generalized Rayleigh quotient is positively proportional to the vector
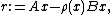
called the eigenvector residual. If a preconditioner
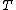is available, it is applied to the residual giving vector
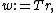
called the preconditioned residual. Without preconditioning, we set
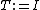and so 
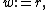. An iterative method
or, in short,
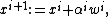
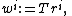
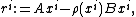
is known as preconditioned steepest accent (or descent), where the scalar
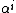is called the step size. The optimal step size can be determined by maximizing the Rayleigh quotient, i.e.,
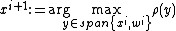
(or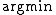
in case of minimizing),
in which case the method is called locally optimal. To further accelerate the convergence of the locally optimal precondiitoned steepest accent (or descent), one can add one extra vector to the two-term recurrence relation
to make it three-term:
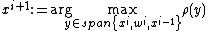
(use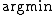
in case of minimizing). The maximization/minimization of the Rayleigh quotient in a 3-dimensional subspace can be performed numerically by the Rayleigh-Ritz method.
This is a single-vector version of the LOBPCG method. It is one of possible generalization of the preconditioned
conjugate gradient
linear solvers to the case of symmetric eigenvalue problems. Even in the trivial case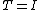
and 
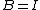the resulting approximation with 
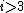will be different from that obtained by the Lanczos algorithm
, although both approximations will belong to the same Krylov subspace
.
Iterating several approximate eigenvectors together in a block in a similar locally optimal fashion, gives the full block version of the LOBPCG. It allows robust computation of eigenvectors corresponding to nearly-multiple eigenvalues.
An implementation of LOBPCG is available in the public software package BLOPEX
, maintained by Andrew Knyazev
. The LOBPCG algorithm is also implemented in many other libraries, e.g.,: ABINIT
, Octopus (software), PESCAN, Anasazi (Trilinos
), SciPy
, NGSolve, and PYFEMax.
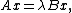
for a given pair
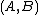of complex Hermitian or real symmetric matrices, wherethe matrix
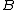is also assumed positive-definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
.
The method performs an iterative maximization (or minimization) of the generalized Rayleigh quotient
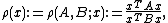
which results in finding largest (or smallest) eigenpairs of
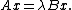
The direction of the steepest accent, which is the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, of the generalized Rayleigh quotient is positively proportional to the vector
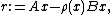
called the eigenvector residual. If a preconditioner
Preconditioner
In mathematics, preconditioning is a procedure of an application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solution. Preconditioning is typically related to reducing a condition number of the problem...
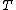is available, it is applied to the residual giving vector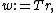called the preconditioned residual. Without preconditioning, we set
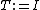and so 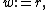. An iterative methodor, in short,
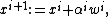
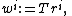
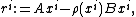
is known as preconditioned steepest accent (or descent), where the scalar
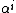is called the step size. The optimal step size can be determined by maximizing the Rayleigh quotient, i.e.,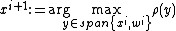(or
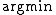in case of minimizing),in which case the method is called locally optimal. To further accelerate the convergence of the locally optimal precondiitoned steepest accent (or descent), one can add one extra vector to the two-term recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
to make it three-term:
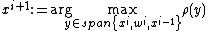
(use
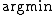in case of minimizing). The maximization/minimization of the Rayleigh quotient in a 3-dimensional subspace can be performed numerically by the Rayleigh-Ritz method.This is a single-vector version of the LOBPCG method. It is one of possible generalization of the preconditioned
Preconditioner
In mathematics, preconditioning is a procedure of an application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solution. Preconditioning is typically related to reducing a condition number of the problem...
conjugate gradient
Conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
linear solvers to the case of symmetric eigenvalue problems. Even in the trivial case
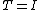and 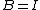the resulting approximation with 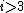will be different from that obtained by the Lanczos algorithmLanczos algorithm
The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...
, although both approximations will belong to the same Krylov subspace
Krylov subspace
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
.
Iterating several approximate eigenvectors together in a block in a similar locally optimal fashion, gives the full block version of the LOBPCG. It allows robust computation of eigenvectors corresponding to nearly-multiple eigenvalues.
An implementation of LOBPCG is available in the public software package BLOPEX
BLOPEX
The Block Locally Optimal Preconditioned Eigenvalue Xolvers is a suite of routines for the scalable solution of eigenvalue problems. Its object-oriented design allows easy portability. Currently available built-in interfaces are Hypre, PETSc, MATLAB, GNU Octave, and a serial stand-alone version...
, maintained by Andrew Knyazev
Andrei Knyazev (mathematician)
Andrei Knyazev is a Russian-American mathematician. He graduated from the Moscow State University under the supervision of Evgenii Georgievich D'yakonov in 1981 and obtained his PhD in Numerical Mathematics at the Russian Academy of Sciences under the supervision of Vyacheslav Ivanovich Lebedev in...
. The LOBPCG algorithm is also implemented in many other libraries, e.g.,: ABINIT
ABINIT
ABINIT is an open-source suite of programs for materials science, distributed under the GNU General Public License. ABINIT implements density functional theory, using a plane wave basis set and pseudopotentials, to compute the electronic density and derived properties of materials ranging from...
, Octopus (software), PESCAN, Anasazi (Trilinos
Trilinos
Trilinos is a collection of open source software libraries, called packages, intended to be used as building blocks for the development of scientific applications...
), SciPy
SciPy
SciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...
, NGSolve, and PYFEMax.