LIBOR Market Model
Encyclopedia
The LIBOR market model, also known as the BGM Model (Brace Gatarek Musiela Model, in reference of the names of some of the inventors), is a financial model of interest rates. It is used for pricing interest rate derivative
s, especially exotic derivatives like Bermudan swaptions, ratchet caps and floors, target redemption notes, autocaps, zero coupon swaptions, constant maturity swaps and spread options, among many others. The quantities that are modeled, rather than the short rate
or instantaneous forward rates (like in the Heath-Jarrow-Morton framework
) are a set of forward rates (also called forward LIBORs), which have the advantage of being directly observable in the market, and whose volatilities are naturally linked to traded contracts. Each forward rate is modeled by a lognormal process under its forward measure
, i.e. a Black model
leading to a Black formula for interest rate caps. This formula is the market standard to quote cap prices in terms of implied volatilities, hence the term "market model". The LIBOR market model may be interpreted as a collection of forward LIBOR dynamics for different forward rates with spanning tenors and maturities, each forward rate being consistent with a Black interest rate caplet formula for its canonical maturity. One can write the different rates dynamics under a common pricing measure
, for example the forward measure
for a preferred single maturity, and in this case forward rates will not be lognormal under the unique measure in general, leading to the need of numerical methods such as monte carlo simulation or approximations like the frozen drift assumption.
forward rates 
, 
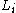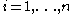as lognormal processes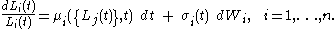
Here,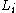
denotes the forward rate for the period 
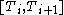. For each single forward rate the model corresponds to the Black model. The novelty is that, in contrast to the Black model, the LIBOR market model describes the dynamic of a whole family of forward rates under a common measure.
Interest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
s, especially exotic derivatives like Bermudan swaptions, ratchet caps and floors, target redemption notes, autocaps, zero coupon swaptions, constant maturity swaps and spread options, among many others. The quantities that are modeled, rather than the short rate
Short rate model
In the context of interest rate derivatives, a short-rate model is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,.-The short rate:...
or instantaneous forward rates (like in the Heath-Jarrow-Morton framework
Heath-Jarrow-Morton framework
The Heath–Jarrow–Morton framework is a general framework to model the evolution of interest rate curve – instantaneous forward rate curve in particular . When the volatility and drift of the instantaneous forward rate are assumed to be deterministic, this is known as the Gaussian...
) are a set of forward rates (also called forward LIBORs), which have the advantage of being directly observable in the market, and whose volatilities are naturally linked to traded contracts. Each forward rate is modeled by a lognormal process under its forward measure
Forward measure
In finance, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure but rather than using the money market as numeraire, it uses a bond with maturity T...
, i.e. a Black model
Black model
The Black model is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing bond options, interest rate caps / floors, and swaptions...
leading to a Black formula for interest rate caps. This formula is the market standard to quote cap prices in terms of implied volatilities, hence the term "market model". The LIBOR market model may be interpreted as a collection of forward LIBOR dynamics for different forward rates with spanning tenors and maturities, each forward rate being consistent with a Black interest rate caplet formula for its canonical maturity. One can write the different rates dynamics under a common pricing measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, for example the forward measure
Forward measure
In finance, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure but rather than using the money market as numeraire, it uses a bond with maturity T...
for a preferred single maturity, and in this case forward rates will not be lognormal under the unique measure in general, leading to the need of numerical methods such as monte carlo simulation or approximations like the frozen drift assumption.
Model dynamic
The LIBOR market model models a set of forward rates 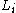, 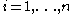as lognormal processes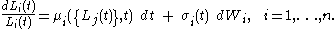Here,
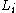denotes the forward rate for the period 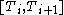. For each single forward rate the model corresponds to the Black model. The novelty is that, in contrast to the Black model, the LIBOR market model describes the dynamic of a whole family of forward rates under a common measure.External links
- Java applets for pricing under a LIBOR market model and Monte-Carlo methods
- Sample chapters of the book "Mathematical Finance" (ISBN 0470047224), with, e.g.,, a derivation of the LIBOR market model drift.
- Damiano Brigo's lecture notes on the LIBOR market model for the Bocconi University fixed income course