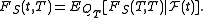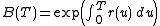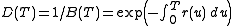Forward measure
Encyclopedia
In finance
, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure
but rather than using the money market as numeraire
, it uses a bond with maturity T. The use of the forward measure was pioneered by Jamshidian (1987), and later used as a means of calculating the price options on bonds .
be the bank account or money market account numeraire and
be the discount factor in the market at time 0 for maturity T. If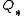
is the risk neutral measure, then the forward measure 
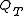is defined via the Radon–Nikodym derivative given by
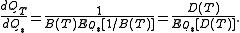
Note that this implies that the forward measure and the risk neutral measure coincide when interest rates are deterministic. Also, this is a particular form of the change of numeraire
formula by changing the numeraire from the money market or bank account B(t) to a T-maturity bond P(t,T). Indeed, if in general
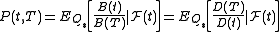
is the price of a zero coupon bond at time t for maturity T, where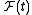
is the filtration denoting market information at time t, then we can write
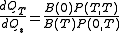
from which it is indeed clear that the forward T measure is associated to the T-maturity zero coupon bond as numeraire
. For a more detailed discussion see Brigo and Mercurio (2001).
s are martingales
, a fact first observed by Geman (1989) (who is responsible for formally defining the measure). Compare with futures prices, which are martingales under the risk neutral measure. Note that when interest rates are deterministic, this implies that forward prices and futures prices are the same.
For example, the discounted stock price is a martingale under the risk-neutral measure:
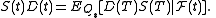
The forward price is given by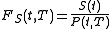
. Thus, we have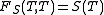 
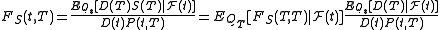
by the abstract Bayes' rule
. The last term is equal to unity by definition of the bond price so that we get
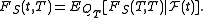
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
but rather than using the money market as numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
, it uses a bond with maturity T. The use of the forward measure was pioneered by Jamshidian (1987), and later used as a means of calculating the price options on bonds .
Mathematical definition
Let
be the bank account or money market account numeraire and
be the discount factor in the market at time 0 for maturity T. If
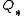is the risk neutral measure, then the forward measure 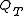is defined via the Radon–Nikodym derivative given by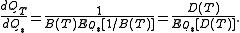Note that this implies that the forward measure and the risk neutral measure coincide when interest rates are deterministic. Also, this is a particular form of the change of numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
formula by changing the numeraire from the money market or bank account B(t) to a T-maturity bond P(t,T). Indeed, if in general
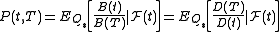
is the price of a zero coupon bond at time t for maturity T, where
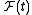is the filtration denoting market information at time t, then we can write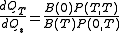from which it is indeed clear that the forward T measure is associated to the T-maturity zero coupon bond as numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
. For a more detailed discussion see Brigo and Mercurio (2001).
Consequences
The name "forward measure" comes from the fact that under the forward measure, forward priceForward price
The forward price is the agreed upon price of an asset in a forward contract. Using the rational pricing assumption, for a forward contract on an underlying asset that is tradeable, we can express the forward price in terms of the spot price and any dividends etc...
s are martingales
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
, a fact first observed by Geman (1989) (who is responsible for formally defining the measure). Compare with futures prices, which are martingales under the risk neutral measure. Note that when interest rates are deterministic, this implies that forward prices and futures prices are the same.
For example, the discounted stock price is a martingale under the risk-neutral measure:
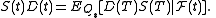
The forward price is given by
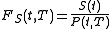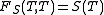
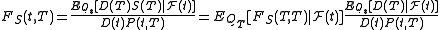
. Thus, we have by the abstract Bayes' rule
Bayes' rule
In probability theory and applications, Bayes' rule relates the odds of event A_1 to event A_2, before and after conditioning on event B. The relationship is expressed in terms of the Bayes factor, \Lambda. Bayes' rule is derived from and closely related to Bayes' theorem...
. The last term is equal to unity by definition of the bond price so that we get