Axiom schema of predicative separation
Encyclopedia
In axiomatic set theory, the axiom schema of predicative separation, or of restricted, or Δ0 separation, is a schema of axiom
s which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset
of a set if that subset can be defined without reference to the entire universe
of sets. The axiom appears in the systems of constructive set theory
CST and CZF, as well as in the system of Kripke-Platek set theory. The name Δ0 comes from the Levy hierarchy (in analogy with the arithmetic hierarchy).
The formal statement of this is the same as full separation schema, but with a restriction on the formulas that may be used. For any formula φ:
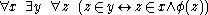
provided, as usual, that the variable y is not free in φ; but also provided that φ contains only bounded quantifiers. That is, all quantifiers in φ (if there are any) must appear in the form
or 
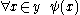for some sub-formula ψ.
The meaning of this is that, given any set x, and any predicate φ there is a set y whose elements are the elements of x which satisfy φ, provided φ only quantifies over existing sets, and never quantifies over all sets. This restriction is necessary from a predicative point of view, since the universe of all sets contains the set being defined. If it were referenced in the definition of the set, the definition would be circular.
Although the schema contains one axiom for each restricted formula φ, it is possible in CZF to replace this schema with a finite number of axioms.
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a set if that subset can be defined without reference to the entire universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
of sets. The axiom appears in the systems of constructive set theory
Constructive set theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...
CST and CZF, as well as in the system of Kripke-Platek set theory. The name Δ0 comes from the Levy hierarchy (in analogy with the arithmetic hierarchy).
The formal statement of this is the same as full separation schema, but with a restriction on the formulas that may be used. For any formula φ:
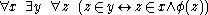
provided, as usual, that the variable y is not free in φ; but also provided that φ contains only bounded quantifiers. That is, all quantifiers in φ (if there are any) must appear in the form
or 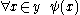for some sub-formula ψ.The meaning of this is that, given any set x, and any predicate φ there is a set y whose elements are the elements of x which satisfy φ, provided φ only quantifies over existing sets, and never quantifies over all sets. This restriction is necessary from a predicative point of view, since the universe of all sets contains the set being defined. If it were referenced in the definition of the set, the definition would be circular.
Although the schema contains one axiom for each restricted formula φ, it is possible in CZF to replace this schema with a finite number of axioms.