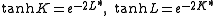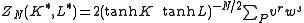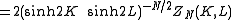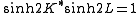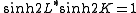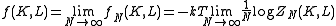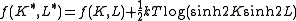Kramers-Wannier duality
Encyclopedia
The Kramers–Wannier duality is a symmetry
in statistical physics
. It relates the free energy
of a two-dimensional square-lattice Ising model
at a low temperature to that of another Ising model at a high temperature. It was discovered by Hendrik Kramers
and Gregory Wannier
in 1941. With the aid of this duality Kramers and Wannier found the exact location of the critical point
for the Ising model on the square lattice.
Similar dualities establish relations between free energies of other statistical models. For instance, in 3 dimensions the Ising model is dual to an Ising gauge model.
suggested that the Star-Triangle transformation could be used for the triangular lattice. Now the dual of the discrete torus is itself. Moreover, the dual of a highly disordered system (high temperature) is a well ordered system (low temperature). This is because the fourier transform takes a high bandwidth signal (more standard deviation
) to a low one (less standard deviation). So one has essentially the same theory with an inverse temperature.
When one raises the temperature in one theory, one lowers the temperature in the other. If there is only one phase transition
, it will be at the point at which they cross, at which the temperature is equal. Because the 2D Ising model goes from a disordered state to an ordered state, there is a near one-to-one mapping between the disordered and ordered phases.
The theory has been generalized, and is now blended with many other ideas. For instance, the square lattice is replaced by a circle, random lattice, nonhomogenous torus, triangular lattice, labyrinth, lattices with twisted boundaries, chiral potts model, and many others.
The low temperature expansion for (K*,L*) is
which by using the transformation
gives
where v = tanh K and w = tanh L. This yields a relation with the high-temperature expansion. The relations can be written more symmetrically as
With the free energy per site in the thermodynamic limit
the Kramers–Wannier duality gives
In the isotropic case where K = L, if there is a critical point at K = Kc then there is another at K = K*c. Hence, in the case of there being a unique critical point, it would be located at K = K* = K*c, implying sinh 2Kc = 1, yielding kTc = 2.2692J.
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
. It relates the free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
of a two-dimensional square-lattice Ising model
Square-lattice Ising model
In statistical mechanics, the two-dimensional square-lattice Ising model was solved by for the special case that the external field H = 0. A solution for the general case for H \neq 0 has yet to be found.-Definition of the model:...
at a low temperature to that of another Ising model at a high temperature. It was discovered by Hendrik Kramers
Hendrik Anthony Kramers
Hendrik Anthony "Hans" Kramers was a Dutch physicist.-Background and education:...
and Gregory Wannier
Gregory Wannier
Gregory Hugh Wannier was a Swiss physicist.He attended Princeton as a graduate student and later taught at several American universities before a stint in industry....
in 1941. With the aid of this duality Kramers and Wannier found the exact location of the critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
for the Ising model on the square lattice.
Similar dualities establish relations between free energies of other statistical models. For instance, in 3 dimensions the Ising model is dual to an Ising gauge model.
Intuitive idea
The 2-dimensional Ising model exists on a lattice, which is a collection of squares in a chessboard pattern. With the finite lattice, the edges can be connected to form a torus. In theories of this kind, one constructs an involutive transform. For instance, Lars OnsagerLars Onsager
Lars Onsager was a Norwegian-born American physical chemist and theoretical physicist, winner of the 1968 Nobel Prize in Chemistry.He held the Gibbs Professorship of Theoretical Chemistry at Yale University....
suggested that the Star-Triangle transformation could be used for the triangular lattice. Now the dual of the discrete torus is itself. Moreover, the dual of a highly disordered system (high temperature) is a well ordered system (low temperature). This is because the fourier transform takes a high bandwidth signal (more standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
) to a low one (less standard deviation). So one has essentially the same theory with an inverse temperature.
When one raises the temperature in one theory, one lowers the temperature in the other. If there is only one phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
, it will be at the point at which they cross, at which the temperature is equal. Because the 2D Ising model goes from a disordered state to an ordered state, there is a near one-to-one mapping between the disordered and ordered phases.
The theory has been generalized, and is now blended with many other ideas. For instance, the square lattice is replaced by a circle, random lattice, nonhomogenous torus, triangular lattice, labyrinth, lattices with twisted boundaries, chiral potts model, and many others.
Derivation
Define these variables.The low temperature expansion for (K*,L*) is
which by using the transformation
gives
where v = tanh K and w = tanh L. This yields a relation with the high-temperature expansion. The relations can be written more symmetrically as
With the free energy per site in the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
the Kramers–Wannier duality gives
In the isotropic case where K = L, if there is a critical point at K = Kc then there is another at K = K*c. Hence, in the case of there being a unique critical point, it would be located at K = K* = K*c, implying sinh 2Kc = 1, yielding kTc = 2.2692J.