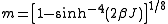
Square-lattice Ising model
Encyclopedia
In statistical mechanics
, the two-dimensional square-lattice Ising model
was solved by for the special case that the external field H = 0. A solution for the general case for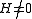
has yet to be found.
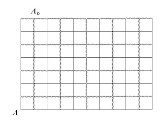
on a square lattice
with N sites, with periodic boundary conditions in both the horizontal and vertical directions, which effectively reduces the geometry
of the model to a torus
. In a general case, the horizontal coupling
J is not equal to the coupling in the vertical direction, J*. With an equal number of rows and columns in the lattice, there will be N of each. In terms of
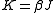
where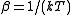
where T is absolute temperature and k is Boltzmann's constant, the partition function
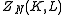is given by
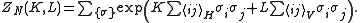
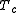can be obtained from the Kramers–Wannier duality relation. Denoting the free energy per site as 
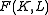, we have:
where
Assuming there is only one critical line in the (K,L) plane, the duality realtion implies that this is given by:
For the isotropic case
, one finds the famous relation for the critical temperature 
.
on the square lattice 
. Let r and s denote the number of unlike neighbours in the vertical and horizontal directions respectively. Then the summand in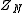 
corresponding to 
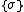is given by
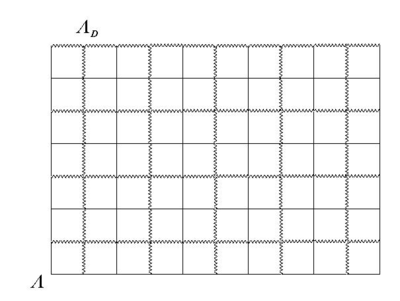Construct a dual lattice 
as depicted in the diagram. For every configuration 
, a polygon is associated to the lattice by drawing a line on the edge of the dual lattice if the spins separated by the edge are unlike. Since by traversing a vertex of 
the spins need to change an even number of times so that one arrives at the starting point with the same charge, every vertex of the dual lattice is connected to an even number of lines in the configuration, defining a polygon.
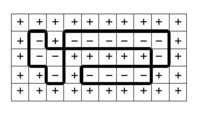This reduces the partition function
to
summing over all polygons in the dual lattice, where r and s are the number of horizontal and vertical lines in the polygon, with the factor of 2 arising from the inversion of spin configuration.
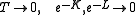, so that
defines a low temperature expansion of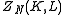
.
one has
Therefore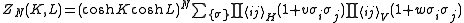
where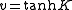
and 
. Since there are N horizontal and vertical edges, there are a total of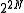 
terms in the expansion. Every term corresponds to a configuration of lines of the lattice, by associating a line connecting i and j if the term 
(or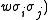 
is chosen in the product. Summing over the configurations, using
shows that only configurations with an even number of lines at each vertex (polygons) will contribute to the partition function, giving
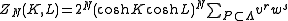
where the sum is over all polygons in the lattice. Since tanh K, tanh L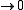
as 
, this gives the high temperature expansion of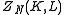 
.
The two expansions can be related using the Kramers-Wannier duality
.
is given as follows. Define the parameter k as:
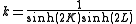
The free energy per site F can be expressed as:
For the isotropic case
, from the above expression one finds for the internal energy per site:
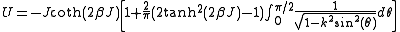
and the spontaneous magnetization is, for
:
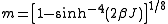
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the two-dimensional square-lattice Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
was solved by for the special case that the external field H = 0. A solution for the general case for
has yet to be found.Definition of the model
Consider the 2D Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
on a square lattice
with N sites, with periodic boundary conditions in both the horizontal and vertical directions, which effectively reduces the geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
of the model to a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. In a general case, the horizontal coupling
Coupling
A coupling is a device used to connect two shafts together at their ends for the purpose of transmitting power. Couplings do not normally allow disconnection of shafts during operation, however there are torque limiting couplings which can slip or disconnect when some torque limit is exceeded.The...
J is not equal to the coupling in the vertical direction, J*. With an equal number of rows and columns in the lattice, there will be N of each. In terms of
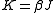
where
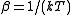where T is absolute temperature and k is Boltzmann's constant, the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
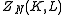is given by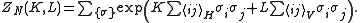Critical temperature
The critical temperature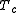 can be obtained from the Kramers–Wannier duality relation. Denoting the free energy per site as 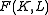, we have:where
Assuming there is only one critical line in the (K,L) plane, the duality realtion implies that this is given by:
For the isotropic case
, one finds the famous relation for the critical temperature .Dual lattice
Consider a configuration of spins on the square lattice . Let r and s denote the number of unlike neighbours in the vertical and horizontal directions respectively. Then the summand in 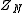corresponding to 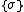is given by as depicted in the diagram. For every configuration , a polygon is associated to the lattice by drawing a line on the edge of the dual lattice if the spins separated by the edge are unlike. Since by traversing a vertex of the spins need to change an even number of times so that one arrives at the starting point with the same charge, every vertex of the dual lattice is connected to an even number of lines in the configuration, defining a polygon.Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
to
summing over all polygons in the dual lattice, where r and s are the number of horizontal and vertical lines in the polygon, with the factor of 2 arising from the inversion of spin configuration.
Low-temperature expansion
At low temperatures, K, L approach infinity, so that as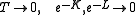, so thatdefines a low temperature expansion of
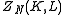.High-temperature expansion
Since one hasTherefore
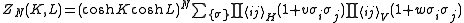
where
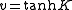and . Since there are N horizontal and vertical edges, there are a total of 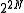terms in the expansion. Every term corresponds to a configuration of lines of the lattice, by associating a line connecting i and j if the term (or 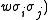is chosen in the product. Summing over the configurations, usingshows that only configurations with an even number of lines at each vertex (polygons) will contribute to the partition function, giving
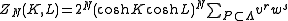
where the sum is over all polygons in the lattice. Since tanh K, tanh L
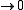as , this gives the high temperature expansion of 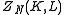.The two expansions can be related using the Kramers-Wannier duality
Kramers-Wannier duality
The Kramers–Wannier duality is a symmetry in statistical physics. It relates the free energy of a two-dimensional square-lattice Ising model at a low temperature to that of another Ising model at a high temperature. It was discovered by Hendrik Kramers and Gregory Wannier in 1941...
.
Exact solution
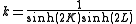
The free energy per site in the limit is given as follows. Define the parameter k as:The free energy per site F can be expressed as:
For the isotropic case
, from the above expression one finds for the internal energy per site: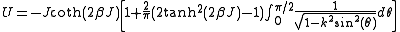and the spontaneous magnetization is, for
: