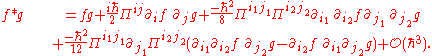Kontsevich quantization formula
Encyclopedia
In mathematics, the Kontsevich quantization formula describes how to construct an generalized ∗-product
operator algebra from a given Poisson manifold
. This operator algebra amounts to the deformation quantization
of the Poisson algebra. It is due to Maxim Kontsevich
.
(A, {.,.}), a deformation
quantization is an associative unital product ∗ on the algebra of formal power series in ħ, A[ [ ħ ] ], subject to the following two axioms,
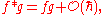
and
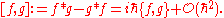
If one were given a Poisson manifold (M, {.,.}), one could ask, in addition, that
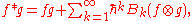
where the Bk are linear bidifferential operator
s of degree at most k.
Two deformations are said to be equivalent iff they are related by a gauge transformation of the type,
where Dn are differential operators of order at most n.
The corresponding induced ∗-product, ∗', is
For the archetypal example, one may well consider Groenewold
's original "Moyal–Weyl" ∗-product
.
without loops on 2 external vertices, labeled f and g; and n internal vertices, labeled Π. From each internal vertex originate two edges. All (equivalence classes of) graphs with n internal vertices are accumulated in the set Gn(2).
An example on two internal vertices is the following graph,
The term for the example graph is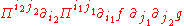 .
.
In order to compute the weight we have to integrate products of the angle in the upper half-plane, H, as follows. The upper half-plane is H⊂ℂ, endowed with a metric
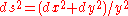 ; and, for two points z, w ∈ H with z ≠ w, we measure the angle φ between the geodesic from z to i∞ and from z to w counterclockwise. This is
; and, for two points z, w ∈ H with z ≠ w, we measure the angle φ between the geodesic from z to i∞ and from z to w counterclockwise. This is
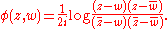
The integration domain is Cn(H) the space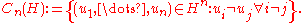
The formula amounts ,
,
where t1(j) and t2(j) are the first and second target vertex of the internal vertex j. The vertices f and g are at the fixed positions 0 and 1 in H.
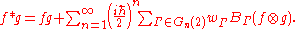
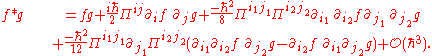
Moyal product
In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
operator algebra from a given Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
. This operator algebra amounts to the deformation quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
of the Poisson algebra. It is due to Maxim Kontsevich
Maxim Kontsevich
Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...
.
Deformation quantization of a Poisson algebra
Given a Poisson algebraPoisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
(A, {.,.}), a deformation
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
quantization is an associative unital product ∗ on the algebra of formal power series in ħ, A[ [ ħ ] ], subject to the following two axioms,
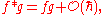
and
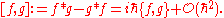
If one were given a Poisson manifold (M, {.,.}), one could ask, in addition, that
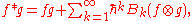
where the Bk are linear bidifferential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s of degree at most k.
Two deformations are said to be equivalent iff they are related by a gauge transformation of the type,

where Dn are differential operators of order at most n.
The corresponding induced ∗-product, ∗', is

For the archetypal example, one may well consider Groenewold
Hilbrand J. Groenewold
Hilbrand Johannes Groenewold was a Dutch theoretical physicist who pioneered the largely operator-free formulation of quantum mechanics in phase space known as phase-space quantization....
's original "Moyal–Weyl" ∗-product
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
.
Kontsevich graphs
A Kontsevich graph is a simple directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
without loops on 2 external vertices, labeled f and g; and n internal vertices, labeled Π. From each internal vertex originate two edges. All (equivalence classes of) graphs with n internal vertices are accumulated in the set Gn(2).
An example on two internal vertices is the following graph,
Associated bidifferential operator
Associated to each graph Γ, there is a bidifferential operator BΓ(f, g) defined as follows. For each edge there is a partial derivative on the symbol of the target vertex. It is contracted with the corresponding index from the source symbol. The term for the graph Γ is the product of all its symbols together with their partial derivatives. Here f and g stand for smooth functions on the manifold, and Π is the Poisson bivector of the Poisson manifold.The term for the example graph is
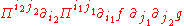 .
.Associated weight
For adding up these bidifferential operators there are the weights wΓ of the graph Γ. First of all, to each graph there is a multiplicity m(Γ) which counts how many equivalent configurations there are for one graph. The rule is that the sum of the multiplicities for all graphs with n internal vertices is (n(n + 1))n. The sample graph above has the weight m(Γ) = 8; for this, it is helpful to enumerate the internal vertices from 1 to n.In order to compute the weight we have to integrate products of the angle in the upper half-plane, H, as follows. The upper half-plane is H⊂ℂ, endowed with a metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
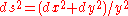 ; and, for two points z, w ∈ H with z ≠ w, we measure the angle φ between the geodesic from z to i∞ and from z to w counterclockwise. This is
; and, for two points z, w ∈ H with z ≠ w, we measure the angle φ between the geodesic from z to i∞ and from z to w counterclockwise. This is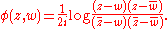
The integration domain is Cn(H) the space
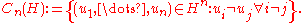
The formula amounts
 ,
,where t1(j) and t2(j) are the first and second target vertex of the internal vertex j. The vertices f and g are at the fixed positions 0 and 1 in H.
The formula
Given the above three definitions, the Kontsevich formula for a star product is now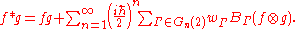
Formula up to second order
Enforcing associativity of the ∗-product, it is easy to check directly that the Kontsevich formula must reduce to second order in ħ to just