
Kolmogorov–Zurbenko filter
Encyclopedia
Kolmogorov–Zurbenko Filter was first proposed by Kolmogorov and formally defined by Zurbenko. It is  time iteration
time iteration
s of a moving average filter of points and belongs to the class of low pass
points and belongs to the class of low pass
filter. KZ filter has two parameters, the length of the moving average window and the number of iterations.
Mathematically, KZ filer can be defined as following. Let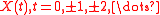 , be a real-valued
, be a real-valued
time series
, KZ filter with parameter
s and
and  is:
is:
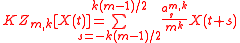
where are given by the polynomial
are given by the polynomial
coefficient
s of
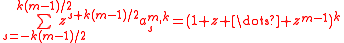
KZ filter can also be obtained through iterations.
1) First iteration is to apply a moving average filter of length ,
,
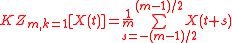
2) Second iteration is to apply the same moving average filter to the result of first iteration,

3)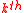 iteration,
iteration,
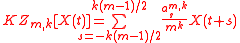
The coefficients of KZ filter,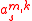 , can be interpreted as a distribution
, can be interpreted as a distribution
obtained by the convolution
of uniform discrete distributions on the interval
uniform discrete distributions on the interval  , where
, where  is an odd integer. Therefore, the coefficient
is an odd integer. Therefore, the coefficient 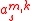 forms a tapering window
forms a tapering window
which has finite support . KZ filter has main weight concentrated on a length of
. KZ filter has main weight concentrated on a length of 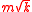 , with weights vanishing to zero outside. The impulse response
, with weights vanishing to zero outside. The impulse response
function of KZ filter has continuous derivatives and is asymptotically
continuous derivatives and is asymptotically
Gaussian distributed. Zero derivatives at the edges of the impulse response function make it a sharply declining function, providing high frequency resolution.
The energy transfer
function of KZ filter is . It is a low-pass filter with cut-off frequency of
. It is a low-pass filter with cut-off frequency of 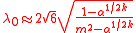 , where
, where  is a pre-specified value.
is a pre-specified value.
KZ filter can be used to smooth the periodogram
. For a class of stochastic process
es, Zurbenko considered the worst case scenario where the only information available about a process is its spectral density
and smoothness quantified by Holder condition. He derived the optimal bandwidth of the spectral window, which is dependent upon the underlying smoothness of the spectral density. Zurbenko compared the performance of Kolmogorov-Zurbenko (KZ) window to the other typically used spectral windows including Bartlett window, Parzen window, Tukey-Hamming window and uniform window and showed that the result from KZ window is closest to optimum.
Extensions of KZ filter include KZ adaptive (KZA) filter, spatial KZ filter and KZ Fourier transform (KZFT). Yang and Zurbenko provided a detailed review of KZ filter and its extensions. R packages are also available to implement KZ filtration. For most recent applications of KZ filtration, please see.
The original idea for the KZ filter was germinated by A. N. Kolmogorov during a study of turbulence in the Pacific Ocean. Kolmogorov had just received the International Boltzano Prize for his law of 2/3 in the power spectra of turbulence. Surprisingly, by our computations, the 2/3 law was not obeyed in the Pacific Ocean, causing great concern. Finally we realized that the regular FFT was completely fooled by the noisy and nonstationary ocean environment. KZ filtration resolved the problem and enabled proof of Kolmogorov's law in the Pacific Ocean. The KZ filter was a unique method for finding information in an extremely noisy and nonstationary background. Filter construction relied on the main concepts of the continuous Fourier transform and their discrete analogues. Algorithm of the KZ filter came from the definition of higher-order derivatives for discrete functions as higher-order differences. Believing that infinite smoothness in the Gaussian window was a beautiful but unrealistic approximation of a truly discrete world, Kolmogorov chose a finitely differentiable tapering window with finite support, and created this mathematical construction for the discrete case. The KZ filter is robust and nearly optimal. Because its operation is a simple moving average, the KZ filter performs well in a missing data environment, especially in multidimensional time and space observations where missing data problem arises from spatial sparseness. Another nice feature of the KZ filter is that the two parameters have clear interpretation so that it can be easily adopted by specialists in different areas. A few software packages for time series, longitudinal and spatial data have been developed in the popular statistical software, R, which facilitate the use of the KZ filter and its extensions in different area.
Developed as an abstract discrete construction, KZ filtration is robust and statistically nearly optimal. At the same time, because of its natural form, it has unbelievable computational advantages, permitting analysis of space/time problems using data that are as much as 90% missing, and which represent a messy combination of several different physical phenomena. Clear answers can often be found for “unsolvable” problems. Unlike some mathematical developments, it is easily adapted by specialists in very different areas because it has a very simple physical sense behind it. Simple and direct adaptive algorithms have been developed in R (KZA) for multidimensional image recognition in time and space.
Pictures were done around the time of turbulence study in the Pacific Ocean.
 time iteration
time iterationIteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
s of a moving average filter of
 points and belongs to the class of low pass
points and belongs to the class of low passLow pass
Low Pass may refer to*Low Pass, Oregon*Low-pass filter* Low Pass in Mountain passes in Montana...
filter. KZ filter has two parameters, the length of the moving average window and the number of iterations.
Mathematically, KZ filer can be defined as following. Let
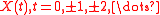 , be a real-valued
, be a real-valuedReal-valued function
In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
, KZ filter with parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s
 and
and  is:
is: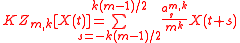
where
 are given by the polynomial
are given by the polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of

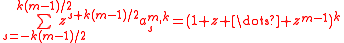
KZ filter can also be obtained through iterations.
1) First iteration is to apply a moving average filter of length
 ,
,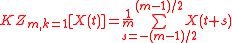
2) Second iteration is to apply the same moving average filter to the result of first iteration,

3)
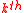 iteration,
iteration,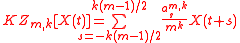
The coefficients of KZ filter,
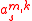 , can be interpreted as a distribution
, can be interpreted as a distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
obtained by the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of
 uniform discrete distributions on the interval
uniform discrete distributions on the interval  , where
, where  is an odd integer. Therefore, the coefficient
is an odd integer. Therefore, the coefficient 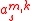 forms a tapering window
forms a tapering windowTapering (mathematics)
In mathematics, physics, and theoretical computer graphics, tapering is a kind of shape deformation. Just as an affine transformation, such as scaling or shearing, is a first-order model of shape deformation, there also exist higher-order deformations such as tapering, twisting, and bending....
which has finite support
 . KZ filter has main weight concentrated on a length of
. KZ filter has main weight concentrated on a length of 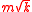 , with weights vanishing to zero outside. The impulse response
, with weights vanishing to zero outside. The impulse responseImpulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
function of KZ filter has
 continuous derivatives and is asymptotically
continuous derivatives and is asymptoticallyAsymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
Gaussian distributed. Zero derivatives at the edges of the impulse response function make it a sharply declining function, providing high frequency resolution.
The energy transfer
Energy transfer
Energy transfer is the transfer of energy from one body to another.There are a few main ways that energy transfer occurs:*Radiant energy *Heat conduction*Convection*Electrical power transmission*Mechanical work...
function of KZ filter is
 . It is a low-pass filter with cut-off frequency of
. It is a low-pass filter with cut-off frequency of 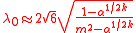 , where
, where  is a pre-specified value.
is a pre-specified value.KZ filter can be used to smooth the periodogram
Periodogram
The periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
. For a class of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, Zurbenko considered the worst case scenario where the only information available about a process is its spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
and smoothness quantified by Holder condition. He derived the optimal bandwidth of the spectral window, which is dependent upon the underlying smoothness of the spectral density. Zurbenko compared the performance of Kolmogorov-Zurbenko (KZ) window to the other typically used spectral windows including Bartlett window, Parzen window, Tukey-Hamming window and uniform window and showed that the result from KZ window is closest to optimum.
Extensions of KZ filter include KZ adaptive (KZA) filter, spatial KZ filter and KZ Fourier transform (KZFT). Yang and Zurbenko provided a detailed review of KZ filter and its extensions. R packages are also available to implement KZ filtration. For most recent applications of KZ filtration, please see.
The original idea for the KZ filter was germinated by A. N. Kolmogorov during a study of turbulence in the Pacific Ocean. Kolmogorov had just received the International Boltzano Prize for his law of 2/3 in the power spectra of turbulence. Surprisingly, by our computations, the 2/3 law was not obeyed in the Pacific Ocean, causing great concern. Finally we realized that the regular FFT was completely fooled by the noisy and nonstationary ocean environment. KZ filtration resolved the problem and enabled proof of Kolmogorov's law in the Pacific Ocean. The KZ filter was a unique method for finding information in an extremely noisy and nonstationary background. Filter construction relied on the main concepts of the continuous Fourier transform and their discrete analogues. Algorithm of the KZ filter came from the definition of higher-order derivatives for discrete functions as higher-order differences. Believing that infinite smoothness in the Gaussian window was a beautiful but unrealistic approximation of a truly discrete world, Kolmogorov chose a finitely differentiable tapering window with finite support, and created this mathematical construction for the discrete case. The KZ filter is robust and nearly optimal. Because its operation is a simple moving average, the KZ filter performs well in a missing data environment, especially in multidimensional time and space observations where missing data problem arises from spatial sparseness. Another nice feature of the KZ filter is that the two parameters have clear interpretation so that it can be easily adopted by specialists in different areas. A few software packages for time series, longitudinal and spatial data have been developed in the popular statistical software, R, which facilitate the use of the KZ filter and its extensions in different area.
Developed as an abstract discrete construction, KZ filtration is robust and statistically nearly optimal. At the same time, because of its natural form, it has unbelievable computational advantages, permitting analysis of space/time problems using data that are as much as 90% missing, and which represent a messy combination of several different physical phenomena. Clear answers can often be found for “unsolvable” problems. Unlike some mathematical developments, it is easily adapted by specialists in very different areas because it has a very simple physical sense behind it. Simple and direct adaptive algorithms have been developed in R (KZA) for multidimensional image recognition in time and space.
Pictures were done around the time of turbulence study in the Pacific Ocean.

