Kenneth Kunen
Encyclopedia
Herbert Kenneth Kunen is an emeritus professor of mathematics
at the University of Wisconsin–Madison
who works in set theory
and its applications to various areas of mathematics, such as set-theoretic topology
and measure theory. He also works on non-associative
algebraic systems, such as loops
, and uses computer software, such as the Otter theorem prover
, to derive theorems in these areas.
Kunen showed that if there exists a nontrivial elementary embedding j:L→L of the constructible universe
, then 0#
holds.
He proved the consistency of a normal,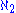
-saturated ideal on 
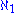from the consistency of the existence of a huge cardinal. He introduced the method of iterated ultrapowers, with which he proved that if 
is a measurable cardinal
with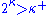
or κ is a strongly compact cardinal
then there is an inner model
of set theory with
many measurable cardinals. He proved Kunen's inconsistency theorem
showing the impossibility of a nontrivial elementary embedding
, which had been suggested as a large cardinal assumption (a Reinhardt cardinal
).
Kunen received his Ph.D.
in 1968 from Stanford University
, where he was supervised by Dana Scott
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
at the University of Wisconsin–Madison
University of Wisconsin–Madison
The University of Wisconsin–Madison is a public research university located in Madison, Wisconsin, United States. Founded in 1848, UW–Madison is the flagship campus of the University of Wisconsin System. It became a land-grant institution in 1866...
who works in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and its applications to various areas of mathematics, such as set-theoretic topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and measure theory. He also works on non-associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
algebraic systems, such as loops
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
, and uses computer software, such as the Otter theorem prover
Otter theorem prover
Otter is an automated theorem prover developed by William McCune at Argonne National Laboratory in Illinois. Otter was the first widely distributed, high-performance theorem prover for first-order logic, and it pioneered a number of important implementation techniques...
, to derive theorems in these areas.
Kunen showed that if there exists a nontrivial elementary embedding j:L→L of the constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
, then 0#
Zero sharp
In the mathematical discipline of set theory, 0# is the set of true formulas about indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers , or as a subset of the hereditarily finite sets, or as a real number...
holds.
He proved the consistency of a normal,
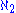-saturated ideal on 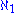from the consistency of the existence of a huge cardinal. He introduced the method of iterated ultrapowers, with which he proved that if is a measurable cardinalMeasurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
with
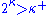or κ is a strongly compact cardinalStrongly compact cardinal
In mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....
then there is an inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
of set theory with
many measurable cardinals. He proved Kunen's inconsistency theoremKunen's inconsistency theorem
In set theory, a branch of mathematics, Kunen's inconsistency theorem, proved by , shows that several plausible large cardinal axioms are inconsistent with the axiom of choice.Some consequences of Kunen's theorem are:...
showing the impossibility of a nontrivial elementary embedding
, which had been suggested as a large cardinal assumption (a Reinhardt cardinalReinhardt cardinal
In set theory, a branch of mathematics, a Reinhardt cardinal is a large cardinal κ, suggested by , that is the critical point of a non-trivial elementary embedding j of V into itself....
).
Kunen received his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
in 1968 from Stanford University
Stanford University
The Leland Stanford Junior University, commonly referred to as Stanford University or Stanford, is a private research university on an campus located near Palo Alto, California. It is situated in the northwestern Santa Clara Valley on the San Francisco Peninsula, approximately northwest of San...
, where he was supervised by Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
.
Selected publications
- The Foundations of Mathematics. College Publications, 2009. ISBN 978-1904987147.
- Set Theory: An Introduction to Independence ProofsSet Theory: An Introduction to Independence ProofsSet Theory: An Introduction to Independence Proofs is an important textbook and reference work in set theory by Kenneth Kunen. It starts from basic notions, including the ZFC axioms, and quickly develops combinatorial notions such as trees, Suslin's problem, ◊, and Martin's axiom...
. North-Holland, 1980. ISBN 0-444-85401-0. - (co-edited with Jerry E. Vaughan). Handbook of Set-Theoretic Topology. North-Holland, 1984. ISBN 0-444-86580-2.