Kahan summation algorithm
Encyclopedia
In numerical analysis
, the Kahan summation algorithm (also known as compensated summation) significantly reduces the numerical error
in the total obtained by adding a sequence
of finite precision floating point numbers, compared to the obvious approach. This is done by keeping a separate running compensation (a variable to accumulate small errors).
In particular, simply summing n numbers in sequence has a worst-case error that grows proportional to n, and a root mean square
error that grows as
for random inputs (the roundoff errors form a random walk
). With compensated summation, the worst-case error bound is independent of n, so a large number of values can be summed with an error that only depends on the floating-point precision
.
The algorithm
is attributed to William Kahan
. Similar, earlier techniques are, for example, Bresenham's line algorithm
, keeping tab of the accumulated error in integer operations (although first documented around the same time) and the Delta-sigma modulation
(integrating, not just summing the error).
, the algorithm is:
function KahanSum(input)
var sum = 0.0
var c = 0.0 //A running compensation for lost low-order bits.
for i = 1 to input.length do
y = input[i] - c //So far, so good: c is zero.
t = sum + y //Alas, sum is big, y small, so low-order digits of y are lost.
c = (t - sum) - y //(t - sum) recovers the high-order part of y; subtracting y recovers -(low part of y)
sum = t //Algebraically, c should always be zero. Beware eagerly optimising compilers!
//Next time around, the lost low part will be added to y in a fresh attempt.
return sum
However, with compensated summation, we get the correct rounded result of 10005.9.
Assume that c has the initial value zero.
y = 3.14159 - 0 y = input[i] - c
t = 10000.0 + 3.14159
= 10003.1 Many digits have been lost!
c = (10003.1 - 10000.0) - 3.14159 This must be evaluated as written!
= 3.10000 - 3.14159 The assimilated part of y recovered, vs. the original full y.
= -.0415900 Trailing zeros shown because this is six-digit arithmetic.
sum = 10003.1 Thus, few digits from input(i) met those of sum.
The sum is so large that only the high-order digits of the input numbers are being accumulated. But on the next step, c gives the error.
y = 2.71828 - -.0415900 The shortfall from the previous stage gets included.
= 2.75987 It is of a size similar to y: most digits meet.
t = 10003.1 + 2.75987 But few meet the digits of sum.
= 10005.85987, rounds to 10005.9
c = (10005.9 - 10003.1) - 2.75987 This extracts whatever went in.
= 2.80000 - 2.75987 In this case, too much.
= .040130 But no matter, the excess would be subtracted off next time.
sum = 10005.9 Exact result is 10005.85987, this is correctly rounded to 6 digits.
So the summation is performed with two accumulators: sum holds the sum, and c accumulates the parts not assimilated into sum, to nudge the low-order part of sum the next time around. Thus the summation proceeds with "guard digits" in c which is better than not having any but is not as good as performing the calculations with double the precision of the input. However, simply increasing the precision of the calculations is not practical in general; if input is already double precision, few systems supply quadruple precision and if they did, input could then be quadruple precision!
Suppose that one is summing n values xi, for i=1,...,n. The exact sum is: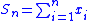
(computed with infinite precision)
With compensated summation, one instead obtains
, where the error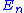 
is bounded above by: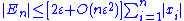
where ε is the machine precision of the arithmetic being employed (e.g. ε≈10−16 for IEEE standard double precision
floating point). Usually, the quantity of interest is the relative error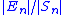
, which is therefore bounded above by: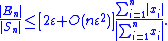
In the expression for the relative error bound, the fraction Σ|xi|/|Σxi| is the condition number
of the summation problem. Essentially, the condition number represents the intrinsic sensitivity of the summation problem to errors, regardless of how it is computed. The relative error bound of every (backwards stable) summation method by a fixed algorithm in fixed precision (i.e. not those that use arbitrary precision arithmetic, nor algorithms whose memory and time requirements change based on the data), is proportional to this condition number. An ill-conditioned summation problem is one in which this ratio is large, and in this case even compensated summation can have a large relative error. For example, if the summands xi are uncorrelated random numbers with zero mean, the sum is a random walk
and the condition number will grow proportional to
. On the other hand, for random inputs with nonzero mean the condition number asymptotes to a finite constant as 
. If the inputs are all non-negative, then the condition number is 1.
Given a condition number, the relative error of compensated summation is effectively independent of n. In principle, there is the O(nε2) that grows linearly with n, but in practice this term is effectively zero: since the final result is rounded to a precision ε, the nε2 term rounds to zero unless n is roughly 1/ε or larger. In double precision, this corresponds to an n of roughly 1016, much larger than most sums. So, for a fixed condition number, the errors of compensated summation are effectively O(ε), independent of n.
In comparison, the relative error bound for naive summation (simply adding the numbers in sequence, rounding at each step) grows as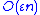
multiplied by the condition number. This worst-case error is rarely observed in practice, however, because it only occurs if the rounding errors are all in the same direction. In practice, it is much more likely that the rounding errors have a random sign, with zero mean, so that they form a random walk; in this case, naive summation has a root mean square
relative error that grows as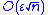
multiplied by the condition number. This is still much worse than compensated summation, however. Note, however, that if the sum can be performed in twice the precision, then ε is replaced by ε2 and naive summation has a worst-case error comparable to the O(nε2) term in compensated summation at the original precision.
By the same token, the Σ|xi| that appears in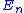
above is a worst-case bound that occurs only if all the rounding errors have the same sign (and are of maximum possible magnitude). In practice, it is more likely that the errors have random sign, in which case terms in Σ|xi| are replaced by a random walk—in this case, even for random inputs with zero mean, the error 
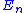grows only as 
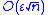(ignoring the nε2 term), the same rate the sum 
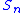grows, canceling the 
factors when the relative error is computed. So, even for asymptotically ill-conditioned sums, the relative error for compensated summation can often be much smaller than a worst-case analysis might suggest.
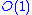error growth for summing n numbers, only slightly worse 
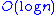growth can be achieved by pairwise summation
: one recursively divides the set of numbers into two halves, sums each half, and then adds the two sums. This has the advantage of requiring the same number of arithmetic operations as the naive summation (unlike Kahan's algorithm, which requires more arithmetic). The base case of the recursion could in principle be the sum of only one (or zero) numbers, but to amortize the overhead of recursion one would normally use a larger base case. The equivalent of pairwise summation is used in many fast Fourier transform
(FFT) algorithms, and is responsible for the logarithmic growth of roundoff errors in those FFTs. In practice, with roundoff errors of random signs, the root mean square errors of cascade summation actually grow as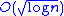
.
Another alternative is to use arbitrary precision arithmetic, which in principle need do no rounding at all at the cost of much greater computational effort. A way of performing exactly rounded sums using arbitrary precision that is extended adaptively using multiple floating-point components, to minimize computational cost in common cases where high precision is not needed, was described by Shewchuk. Another method that uses only integer arithmetic, but a large accumulator was described by Kirchner and Kulisch; a hardware implementation was described by Müller, Rüb and Rülling.
could destroy the effectiveness of Kahan summation: for example, if the compiler simplified expressions according to the associativity
rules of real arithmetic, it might "simplify" the second step in the sequence
is one example that allows associativity-based transformations by default. The original K&R C version of the C programming language allowed the compiler to re-order floating-point expressions according to real-arithmetic associativity rules, but the subsequent ANSI C
standard prohibited re-ordering in order to make C better suited for numerical applications (and more similar to Fortran
, which also prohibits re-ordering), although in practice compiler options can re-enable re-ordering as mentioned above.
In general, built-in "sum" functions in computer languages typically provide no guarantees that a particular summation algorithm will be employed, much less Kahan summation. The BLAS
standard for linear algebra
subroutines explicitly avoids mandating any particular computational order of operations for performance reasons, and BLAS implementations typically do not use Kahan summation.
The standard library of the Python
computer language specifies an fsum function for exactly rounded summation, using the Shewchuk algorithm to track multiple partial sums.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Kahan summation algorithm (also known as compensated summation) significantly reduces the numerical error
Numerical error
In software engineering and mathematics, numerical error is the combined effect of two kinds of error in a calculation. The first is caused by the finite precision of computations involving floating-point or integer values...
in the total obtained by adding a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of finite precision floating point numbers, compared to the obvious approach. This is done by keeping a separate running compensation (a variable to accumulate small errors).
In particular, simply summing n numbers in sequence has a worst-case error that grows proportional to n, and a root mean square
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
error that grows as
for random inputs (the roundoff errors form a random walkRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
). With compensated summation, the worst-case error bound is independent of n, so a large number of values can be summed with an error that only depends on the floating-point precision
Precision (arithmetic)
The precision of a value describes the number of digits that are used to express that value. In a scientific setting this would be the total number of digits or, less commonly, the number of fractional digits or decimal places...
.
The algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is attributed to William Kahan
William Kahan
William Morton Kahan is a mathematician and computer scientist who received the Turing Award in 1989 for "his fundamental contributions to numerical analysis", and was named an ACM Fellow in 1994....
. Similar, earlier techniques are, for example, Bresenham's line algorithm
Bresenham's line algorithm
The Bresenham line algorithm is an algorithm which determines which points in an n-dimensional raster should be plotted in order to form a close approximation to a straight line between two given points...
, keeping tab of the accumulated error in integer operations (although first documented around the same time) and the Delta-sigma modulation
Delta-sigma modulation
Delta-sigma modulation is a method for encoding high-resolution or analog signals into lower-resolution digital signals. The conversion is done using error feedback, where the difference between the two signals is measured and used to improve the conversion...
(integrating, not just summing the error).
The algorithm
In pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
, the algorithm is:
function KahanSum(input)
var sum = 0.0
var c = 0.0 //A running compensation for lost low-order bits.
for i = 1 to input.length do
y = input[i] - c //So far, so good: c is zero.
t = sum + y //Alas, sum is big, y small, so low-order digits of y are lost.
c = (t - sum) - y //(t - sum) recovers the high-order part of y; subtracting y recovers -(low part of y)
sum = t //Algebraically, c should always be zero. Beware eagerly optimising compilers!
//Next time around, the lost low part will be added to y in a fresh attempt.
return sum
Worked example
This example will be given in decimal. Computers typically use binary arithmetic, but the principle being illustrated is the same. Suppose we are using six-digit decimal floating point arithmetic, sum has attained the value 10000.0, and the next two values of input(i) are 3.14159 and 2.71828. The exact result is 10005.85987, which rounds to 10005.9. With a plain summation, each incoming value would be aligned with sum and many low order digits lost (by truncation or rounding.) The first result, after rounding, would be 10003.1. The second result would be 10005.81828 before rounding, and 10005.8 after rounding. This is not correct.However, with compensated summation, we get the correct rounded result of 10005.9.
Assume that c has the initial value zero.
y = 3.14159 - 0 y = input[i] - c
t = 10000.0 + 3.14159
= 10003.1 Many digits have been lost!
c = (10003.1 - 10000.0) - 3.14159 This must be evaluated as written!
= 3.10000 - 3.14159 The assimilated part of y recovered, vs. the original full y.
= -.0415900 Trailing zeros shown because this is six-digit arithmetic.
sum = 10003.1 Thus, few digits from input(i) met those of sum.
The sum is so large that only the high-order digits of the input numbers are being accumulated. But on the next step, c gives the error.
y = 2.71828 - -.0415900 The shortfall from the previous stage gets included.
= 2.75987 It is of a size similar to y: most digits meet.
t = 10003.1 + 2.75987 But few meet the digits of sum.
= 10005.85987, rounds to 10005.9
c = (10005.9 - 10003.1) - 2.75987 This extracts whatever went in.
= 2.80000 - 2.75987 In this case, too much.
= .040130 But no matter, the excess would be subtracted off next time.
sum = 10005.9 Exact result is 10005.85987, this is correctly rounded to 6 digits.
So the summation is performed with two accumulators: sum holds the sum, and c accumulates the parts not assimilated into sum, to nudge the low-order part of sum the next time around. Thus the summation proceeds with "guard digits" in c which is better than not having any but is not as good as performing the calculations with double the precision of the input. However, simply increasing the precision of the calculations is not practical in general; if input is already double precision, few systems supply quadruple precision and if they did, input could then be quadruple precision!
Accuracy
A careful analysis of the errors in compensated summation is needed to appreciate its accuracy characteristics. While it is more accurate than naive summation, it can still give large relative errors for ill-conditioned sums.Suppose that one is summing n values xi, for i=1,...,n. The exact sum is:
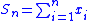(computed with infinite precision)With compensated summation, one instead obtains
, where the error 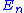is bounded above by: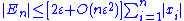where ε is the machine precision of the arithmetic being employed (e.g. ε≈10−16 for IEEE standard double precision
Double precision
In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point .Modern computers with 32-bit storage locations...
floating point). Usually, the quantity of interest is the relative error
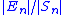, which is therefore bounded above by: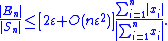In the expression for the relative error bound, the fraction Σ|xi|/|Σxi| is the condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of the summation problem. Essentially, the condition number represents the intrinsic sensitivity of the summation problem to errors, regardless of how it is computed. The relative error bound of every (backwards stable) summation method by a fixed algorithm in fixed precision (i.e. not those that use arbitrary precision arithmetic, nor algorithms whose memory and time requirements change based on the data), is proportional to this condition number. An ill-conditioned summation problem is one in which this ratio is large, and in this case even compensated summation can have a large relative error. For example, if the summands xi are uncorrelated random numbers with zero mean, the sum is a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
and the condition number will grow proportional to
. On the other hand, for random inputs with nonzero mean the condition number asymptotes to a finite constant as . If the inputs are all non-negative, then the condition number is 1.Given a condition number, the relative error of compensated summation is effectively independent of n. In principle, there is the O(nε2) that grows linearly with n, but in practice this term is effectively zero: since the final result is rounded to a precision ε, the nε2 term rounds to zero unless n is roughly 1/ε or larger. In double precision, this corresponds to an n of roughly 1016, much larger than most sums. So, for a fixed condition number, the errors of compensated summation are effectively O(ε), independent of n.
In comparison, the relative error bound for naive summation (simply adding the numbers in sequence, rounding at each step) grows as
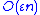multiplied by the condition number. This worst-case error is rarely observed in practice, however, because it only occurs if the rounding errors are all in the same direction. In practice, it is much more likely that the rounding errors have a random sign, with zero mean, so that they form a random walk; in this case, naive summation has a root mean squareRoot mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
relative error that grows as
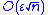multiplied by the condition number. This is still much worse than compensated summation, however. Note, however, that if the sum can be performed in twice the precision, then ε is replaced by ε2 and naive summation has a worst-case error comparable to the O(nε2) term in compensated summation at the original precision.By the same token, the Σ|xi| that appears in
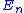above is a worst-case bound that occurs only if all the rounding errors have the same sign (and are of maximum possible magnitude). In practice, it is more likely that the errors have random sign, in which case terms in Σ|xi| are replaced by a random walk—in this case, even for random inputs with zero mean, the error 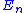grows only as 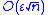(ignoring the nε2 term), the same rate the sum 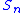grows, canceling the factors when the relative error is computed. So, even for asymptotically ill-conditioned sums, the relative error for compensated summation can often be much smaller than a worst-case analysis might suggest.Alternatives
Although Kahan's algorithm achieves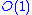 error growth for summing n numbers, only slightly worse 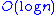growth can be achieved by pairwise summationPairwise summation
In numerical analysis, pairwise summation, also called cascade summation, is a technique to sum a sequence of finite-precision floating-point numbers that substantially reduces the accumulated round-off error compared to naively accumulating the sum in sequence...
: one recursively divides the set of numbers into two halves, sums each half, and then adds the two sums. This has the advantage of requiring the same number of arithmetic operations as the naive summation (unlike Kahan's algorithm, which requires more arithmetic). The base case of the recursion could in principle be the sum of only one (or zero) numbers, but to amortize the overhead of recursion one would normally use a larger base case. The equivalent of pairwise summation is used in many fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithms, and is responsible for the logarithmic growth of roundoff errors in those FFTs. In practice, with roundoff errors of random signs, the root mean square errors of cascade summation actually grow as
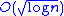.Another alternative is to use arbitrary precision arithmetic, which in principle need do no rounding at all at the cost of much greater computational effort. A way of performing exactly rounded sums using arbitrary precision that is extended adaptively using multiple floating-point components, to minimize computational cost in common cases where high precision is not needed, was described by Shewchuk. Another method that uses only integer arithmetic, but a large accumulator was described by Kirchner and Kulisch; a hardware implementation was described by Müller, Rüb and Rülling.
Computer languages
In principle, a sufficiently aggressive optimizing compilerCompiler optimization
Compiler optimization is the process of tuning the output of a compiler to minimize or maximize some attributes of an executable computer program. The most common requirement is to minimize the time taken to execute a program; a less common one is to minimize the amount of memory occupied...
could destroy the effectiveness of Kahan summation: for example, if the compiler simplified expressions according to the associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
rules of real arithmetic, it might "simplify" the second step in the sequence
t = sum + y; c = (t - sum) - y; to ((sum + y) - sum) - y; then to c = 0;, eliminating the error compensation. In practice, many compilers do not use associativity rules (which are only approximate in floating-point arithmetic) in simplifications unless explicitly directed to do so by compiler options enabling "unsafe" optimizations, although the Intel C++ CompilerIntel C++ Compiler
Intel C++ Compiler is a group of C and C++ compilers from Intel Corporation available for GNU/Linux, Mac OS X, and Microsoft Windows....
is one example that allows associativity-based transformations by default. The original K&R C version of the C programming language allowed the compiler to re-order floating-point expressions according to real-arithmetic associativity rules, but the subsequent ANSI C
ANSI C
ANSI C refers to the family of successive standards published by the American National Standards Institute for the C programming language. Software developers writing in C are encouraged to conform to the standards, as doing so aids portability between compilers.-History and outlook:The first...
standard prohibited re-ordering in order to make C better suited for numerical applications (and more similar to Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
, which also prohibits re-ordering), although in practice compiler options can re-enable re-ordering as mentioned above.
In general, built-in "sum" functions in computer languages typically provide no guarantees that a particular summation algorithm will be employed, much less Kahan summation. The BLAS
Blas
Blas is mainly a Spanish given name and surname, related to Blaise. It may refer to-Places:*Piz Blas, mountain in Switzerland*San Blas , many places - see separate article, also**Cape San Blas Light, lighthouse...
standard for linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
subroutines explicitly avoids mandating any particular computational order of operations for performance reasons, and BLAS implementations typically do not use Kahan summation.
The standard library of the Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
computer language specifies an fsum function for exactly rounded summation, using the Shewchuk algorithm to track multiple partial sums.