Iterative deepening depth-first search
Encyclopedia
Iterative deepening depth-first search (IDDFS) is a state space search
strategy in which a depth-limited search
is run repeatedly, increasing the depth limit with each iteration until it reaches
, the depth of the shallowest goal state. On each iteration, IDDFS visits the node
s in the search tree
in the same order as depth-first search
, but the cumulative order in which nodes are first visited, assuming no pruning
, is effectively breadth-first
.
's space-efficiency and breadth-first search
's completeness (when the branching factor
is finite). It is optimal when the path cost is a non-decreasing function of the depth of the node.
The space complexity of IDDFS is
, where 
is the branching factor and 
is the depth of shallowest goal. Since iterative deepening visits states multiple times, it may seem wasteful, but it turns out to be not so costly, since in a tree most of the nodes are in the bottom level, so it does not matter much if the upper levels are visited multiple times.
The main advantage of IDDFS in game tree
searching is that the earlier searches tend to improve the commonly used heuristics, such as the killer heuristic
and alpha-beta pruning
, so that a more accurate estimate of the score of various nodes at the final depth search can occur, and the search completes more quickly since it is done in a better order. For example, alpha-beta pruning is most efficient if it searches the best moves first.
A second advantage is the responsiveness of the algorithm. Because early iterations use small values for
, they execute extremely quickly. This allows the algorithm to supply early indications of the result almost immediately, followed by refinements as 
increases. When used in an interactive setting, such as in a chess
-playing program, this facility allows the program to play at any time with the current best move found in the search it has completed so far. This is not possible with a traditional depth-first search.
The time complexity
of IDDFS in well-balanced trees works out to be the same as Depth-first search:
.
In an iterative deepening search, the nodes on the bottom level are expanded once, those on the
next to bottom level are expanded twice, and so on, up to the root of the search tree, which is
expanded
times. So the total number of expansions in an iterative deepening search is
For
and 
the number is
All together, an iterative deepening search from depth 1 to depth
expands only about 11% more nodes than a single breadth-first or depth-limited search to depth 
, when 
. The higher the branching factor, the lower the overhead of repeatedly expanded states, but even when the branching factor is 2, iterative deepening search only takes about twice as long as a complete breadth-first search. This means that the time complexity of iterative deepening is still 
, and the space complexity is 
. In general, iterative deepening is the preferred search method when there is a large search space and the depth of the solution is not known.
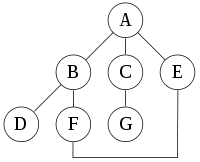
a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree
, a structure with important applications in graph theory
.
Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening prevents this loop and will reach the following nodes on the following depths, assuming it proceeds left-to-right as above:
(Note that iterative deepening has now seen C, when a conventional depth-first search did not.)
(Note that it still sees C, but that it came later. Also note that it sees E via a different path, and loops back to F twice.)
For this graph, as more depth is added, the two cycles "ABFE" and "AEFB" will simply get longer before the algorithm gives up and tries another branch.
-
{
depth = 0
while(no solution)
{
solution = DLS(root, goal, depth)
depth = depth + 1
}
return solution
}
DLS(node, goal, depth)
{
if ( depth >= 0 )
{
if ( node goal )
Related algorithms
Similar to iterative deepening is a search strategy called iterative lengthening search that works with increasing path-cost limits instead of depth-limits. It expands nodes in the order of increasing path cost; therefore the first goal it encounters is the one with the cheapest path cost. But iterative lengthening incurs substantial overhead that make it less useful than iterative deepening.
State space search
State space search is a process used in the field of computer science, including artificial intelligence , in which successive configurations or states of an instance are considered, with the goal of finding a goal state with a desired property....
strategy in which a depth-limited search
Depth-limited search
In computer science depth-limited search is an algorithm to explore the vertices of a graph. It is a modification of depth-first search and is used for example in the iterative deepening depth-first search algorithm.- General :...
is run repeatedly, increasing the depth limit with each iteration until it reaches
, the depth of the shallowest goal state. On each iteration, IDDFS visits the nodeNode (computer science)
A node is a record consisting of one or more fields that are links to other nodes, and a data field. The link and data fields are often implemented by pointers or references although it is also quite common for the data to be embedded directly in the node. Nodes are used to build linked, often...
s in the search tree
Search tree
In computer science, a search tree is a binary tree data structure in whose nodes data values are stored from some ordered set, in such a way that in-order traversal of the tree visits the nodes in ascending order of the stored values...
in the same order as depth-first search
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
, but the cumulative order in which nodes are first visited, assuming no pruning
Pruning (algorithm)
Pruning is a technique in machine learning that reduces the size of decision trees by removing sections of the tree that provide little power to classify instances...
, is effectively breadth-first
Breadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
.
Properties
IDDFS combines depth-first searchDepth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
's space-efficiency and breadth-first search
Breadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
's completeness (when the branching factor
Branching factor
In computing, tree data structures, and game theory, the branching factor is the number of children at each node. If this value is not uniform, an average branching factor can be calculated....
is finite). It is optimal when the path cost is a non-decreasing function of the depth of the node.
The space complexity of IDDFS is
, where is the branching factor and is the depth of shallowest goal. Since iterative deepening visits states multiple times, it may seem wasteful, but it turns out to be not so costly, since in a tree most of the nodes are in the bottom level, so it does not matter much if the upper levels are visited multiple times.The main advantage of IDDFS in game tree
Game tree
In game theory, a game tree is a directed graph whose nodes are positions in a game and whose edges are moves. The complete game tree for a game is the game tree starting at the initial position and containing all possible moves from each position; the complete tree is the same tree as that...
searching is that the earlier searches tend to improve the commonly used heuristics, such as the killer heuristic
Killer heuristic
In competitive two-player games, the killer heuristic is a technique for improving the efficiency of alpha-beta pruning, which in turn improves the efficiency of the minimax algorithm. This algorithm has an exponential search time to find the optimal next move, so general methods for speeding it...
and alpha-beta pruning
Alpha-beta pruning
Alpha-beta pruning is a search algorithm which seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player games...
, so that a more accurate estimate of the score of various nodes at the final depth search can occur, and the search completes more quickly since it is done in a better order. For example, alpha-beta pruning is most efficient if it searches the best moves first.
A second advantage is the responsiveness of the algorithm. Because early iterations use small values for
, they execute extremely quickly. This allows the algorithm to supply early indications of the result almost immediately, followed by refinements as increases. When used in an interactive setting, such as in a chessChess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
-playing program, this facility allows the program to play at any time with the current best move found in the search it has completed so far. This is not possible with a traditional depth-first search.
The time complexity
Time complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
of IDDFS in well-balanced trees works out to be the same as Depth-first search:
.In an iterative deepening search, the nodes on the bottom level are expanded once, those on the
next to bottom level are expanded twice, and so on, up to the root of the search tree, which is
expanded
times. So the total number of expansions in an iterative deepening search isFor
and the number is- 6 + 50 + 400 + 3,000 + 20,000 + 100,000 = 123,456
All together, an iterative deepening search from depth 1 to depth
expands only about 11% more nodes than a single breadth-first or depth-limited search to depth , when . The higher the branching factor, the lower the overhead of repeatedly expanded states, but even when the branching factor is 2, iterative deepening search only takes about twice as long as a complete breadth-first search. This means that the time complexity of iterative deepening is still , and the space complexity is . In general, iterative deepening is the preferred search method when there is a large search space and the depth of the solution is not known.Example
For the following graph:a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree
Trémaux tree
In graph theory a Trémaux tree of a graph G is a spanning tree of G, rooted at one of its vertices, with the property that every edge in G connects a pair of vertices that are related as ancestor and descendant in the tree...
, a structure with important applications in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening prevents this loop and will reach the following nodes on the following depths, assuming it proceeds left-to-right as above:
- 0: A
- 1: A (repeated), B, C, E
(Note that iterative deepening has now seen C, when a conventional depth-first search did not.)
- 2: A, B, D, F, C, G, E, F
(Note that it still sees C, but that it came later. Also note that it sees E via a different path, and loops back to F twice.)
- 3: A, B, D, F, E, C, G, E, F, B
For this graph, as more depth is added, the two cycles "ABFE" and "AEFB" will simply get longer before the algorithm gives up and tries another branch.
-
Pseudocode
IDDFS(root, goal){
depth = 0
while(no solution)
{
solution = DLS(root, goal, depth)
depth = depth + 1
}
return solution
}
DLS(node, goal, depth)
{
if ( depth >= 0 )
{
if ( node
goal )
return node
for each child in expand(node)
DLS(child, goal, depth-1)
}
}
Related algorithms Similar to iterative deepening is a search strategy called iterative lengthening search that works with increasing path-cost limits instead of depth-limits. It expands nodes in the order of increasing path cost; therefore the first goal it encounters is the one with the cheapest path cost. But iterative lengthening incurs substantial overhead that make it less useful than iterative deepening.