Alpha-beta pruning
Encyclopedia
Alpha-beta pruning is a search algorithm
which seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree
. It is an adversarial search algorithm used commonly for machine playing of two-player games (Tic-tac-toe
, Chess
, Go
, etc.). It stops completely evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.
and Herbert Simon
who used what John McCarthy
calls an "approximation" in 1958 wrote that alpha-beta "appears to have been reinvented a number of times". Arthur Samuel
had an early version and Richards, Hart, Levine and/or Edwards found alpha-beta independently in the United States
. McCarthy proposed similar ideas during the Dartmouth Conference
in 1956 and suggested it to a group of his students including Alan Kotok
at MIT in 1961. Alexander Brudno
independently discovered the alpha-beta algorithm, publishing his results in 1963. Donald Knuth
and Ronald W. Moore refined the algorithm in 1975 and it continued to be advanced.
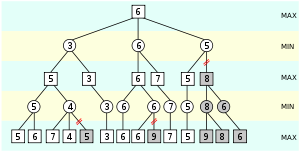The benefit of alpha-beta pruning lies in the fact that branches of the search tree can be eliminated. This way, the search time can be limited to the 'more promising' subtree, and a deeper search can be performed in the same time. Like its predecessor, it belongs to the branch and bound
class of algorithms. The optimization reduces the effective depth to slightly more than half that of simple minimax if the nodes are evaluated in an optimal or near optimal order (best choice for side on move ordered first at each node).
With an (average or constant) branching factor
of b, and a search depth of d plies
, the maximum number of leaf node positions evaluated (when the move ordering is pessimal) is O
(b*b*...*b) = O(bd) – the same as a simple minimax search. If the move ordering for the search is optimal (meaning the best moves are always searched first), the number of leaf node positions evaluated is about O(b*1*b*1*...*b) for odd depth and O(b*1*b*1*...*1) for even depth, or
. In the latter case, where the ply of a search is even, the effective branching factor is reduced to its square root
, or, equivalently, the search can go twice as deep with the same amount of computation. The explanation of b*1*b*1*... is that all the first player's moves must be studied to find the best one, but for each, only the best second player's move is needed to refute all but the first (and best) first player move – alpha-beta ensures no other second player moves need be considered.
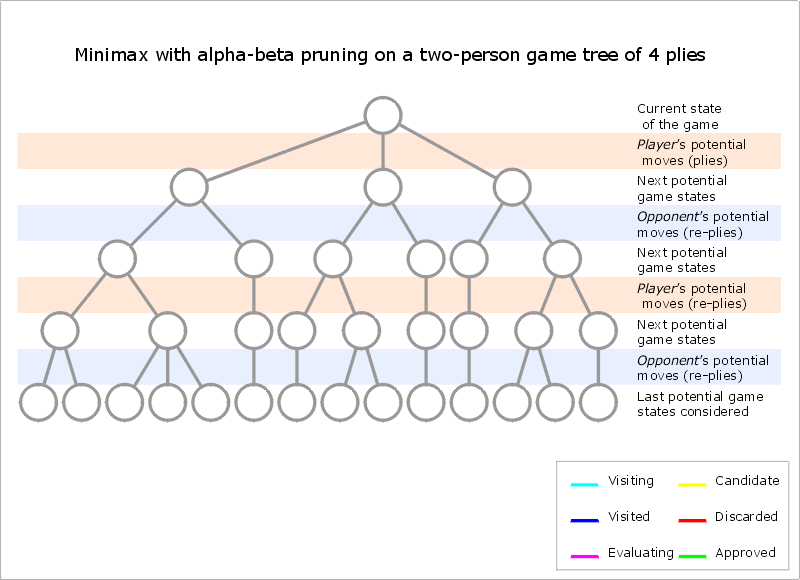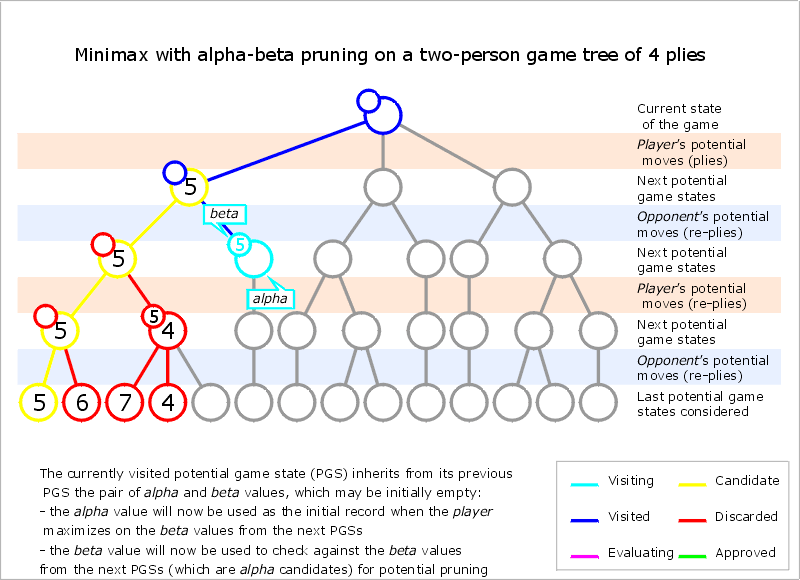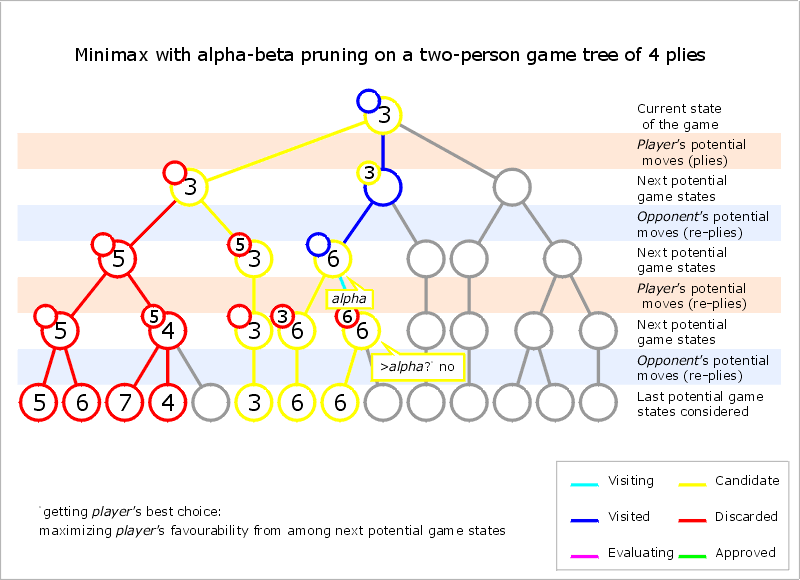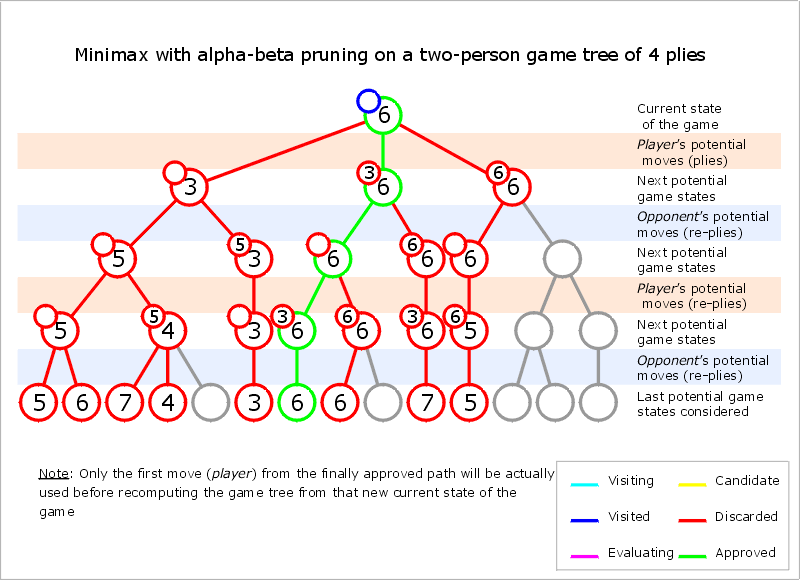Normally during alpha-beta, the subtrees are temporarily dominated by either a first player advantage (when many first player moves are good, and at each search depth the first move checked by the first player is adequate, but all second player responses are required to try and find a refutation), or vice versa. This advantage can switch sides many times during the search if the move ordering is incorrect, each time leading to inefficiency. As the number of positions searched decreases exponentially each move nearer the current position, it is worth spending considerable effort on sorting early moves. An improved sort at any depth will exponentially reduce the total number of positions searched, but sorting all positions at depths near the root node is relatively cheap as there are so few of them. In practice, the move ordering is often determined by the results of earlier, smaller searches, such as through iterative deepening
.
The algorithm maintains two values, alpha and beta, which represent the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of respectively. Initially alpha is negative infinity and beta is positive infinity. As the recursion progresses the "window" becomes smaller. When beta becomes less than alpha, it means that the current position cannot be the result of best play by both players and hence need not be explored further.
Additionally, this algorithm can be trivially modified to return an entire principal variation in addition to the score. Some more aggressive algorithms such as MTD(f) do not easily permit such a modification.
if depth = 0 or node is a terminal node
return the heuristic value of node
if Player = MaxPlayer
for each child of node
α := max(α, alphabeta(child, depth-1, α, β, not(Player) ))
if β ≤ α
break (* Beta cut-off *)
return α
else
for each child of node
β := min(β, alphabeta(child, depth-1, α, β, not(Player) ))
if β ≤ α
break (* Alpha cut-off *)
return β
(* Initial call *)
alphabeta(origin, depth, -infinity, +infinity, MaxPlayer)
s to search parts of the tree that are likely to force alpha-beta cutoffs early. For example, in chess, moves that take pieces may be examined before moves that do not, or moves that have scored highly in earlier passes
through the game-tree analysis may be evaluated before others. Another common, and very cheap, heuristic is the killer heuristic
, where the last move that caused a beta-cutoff at the same level in the tree search is always examined first. This idea can be generalized into a set of refutation tables.
Alpha-beta search can be made even faster by considering only a narrow search window (generally determined by guesswork based on experience). This is known as aspiration search. In the extreme case, the search is performed with alpha and beta equal; a technique known as zero-window search, null-window search, or scout search. This is particularly useful for win/loss searches near the end of a game where the extra depth gained from the narrow window and a simple win/loss evaluation function may lead to a conclusive result. If an aspiration search fails, it is straightforward to detect whether it failed high (high edge of window was too low) or low (lower edge of window was too high). This gives information about what window values might be useful in a re-search of the position.
and MTD-f
.
Since the minimax algorithm and its variants are inherently depth-first
, a strategy such as iterative deepening
is usually used in conjunction with alpha-beta so that a reasonably good move can be returned even if the algorithm is interrupted before it has finished execution. Another advantage of using iterative deepening is that searches at shallower depths give move-ordering hints that can help produce cutoffs for higher depth searches much earlier than would otherwise be possible.
Algorithms like SSS*, on the other hand, use the best-first strategy. This can potentially make them more time-efficient, but typically at a heavy cost in space-efficiency.
Search algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
which seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree
Game tree
In game theory, a game tree is a directed graph whose nodes are positions in a game and whose edges are moves. The complete game tree for a game is the game tree starting at the initial position and containing all possible moves from each position; the complete tree is the same tree as that...
. It is an adversarial search algorithm used commonly for machine playing of two-player games (Tic-tac-toe
Tic-tac-toe
Tic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...
, Chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
, Go
Go (board game)
Go , is an ancient board game for two players that originated in China more than 2,000 years ago...
, etc.). It stops completely evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.
History
Allen NewellAllen Newell
Allen Newell was a researcher in computer science and cognitive psychology at the RAND corporation and at Carnegie Mellon University’s School of Computer Science, Tepper School of Business, and Department of Psychology...
and Herbert Simon
Herbert Simon
Herbert Alexander Simon was an American political scientist, economist, sociologist, and psychologist, and professor—most notably at Carnegie Mellon University—whose research ranged across the fields of cognitive psychology, cognitive science, computer science, public administration, economics,...
who used what John McCarthy
John McCarthy (computer scientist)
John McCarthy was an American computer scientist and cognitive scientist. He coined the term "artificial intelligence" , invented the Lisp programming language and was highly influential in the early development of AI.McCarthy also influenced other areas of computing such as time sharing systems...
calls an "approximation" in 1958 wrote that alpha-beta "appears to have been reinvented a number of times". Arthur Samuel
Arthur Samuel
Arthur Lee Samuel was an American pioneer in the field of computer gaming and artificial intelligence. The Samuel Checkers-playing Program appears to be the world's first self-learning program, and as such a very early demonstration of the fundamental concept of artificial intelligence...
had an early version and Richards, Hart, Levine and/or Edwards found alpha-beta independently in the United States
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
. McCarthy proposed similar ideas during the Dartmouth Conference
Dartmouth Conference
The Dartmouth Summer Research Conference on Artificial Intelligence was the name of a 1956 conference now considered the seminal event for artificial intelligence as a field.-People:...
in 1956 and suggested it to a group of his students including Alan Kotok
Alan Kotok
Alan Kotok was an American computer scientist known for his work at Digital Equipment Corporation and at the World Wide Web Consortium...
at MIT in 1961. Alexander Brudno
Alexander Brudno
Alexander Brudno was a Russian Jewish computer scientist, best known for fully describing the alpha-beta search algorithm...
independently discovered the alpha-beta algorithm, publishing his results in 1963. Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
and Ronald W. Moore refined the algorithm in 1975 and it continued to be advanced.
Improvements over naive minimax
Branch and bound
Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
class of algorithms. The optimization reduces the effective depth to slightly more than half that of simple minimax if the nodes are evaluated in an optimal or near optimal order (best choice for side on move ordered first at each node).
With an (average or constant) branching factor
Branching factor
In computing, tree data structures, and game theory, the branching factor is the number of children at each node. If this value is not uniform, an average branching factor can be calculated....
of b, and a search depth of d plies
Ply (game theory)
In two-player sequential games, a ply refers to one turn taken by one of the players. The word is used to clarify what is meant when one might otherwise say "turn"....
, the maximum number of leaf node positions evaluated (when the move ordering is pessimal) is O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(b*b*...*b) = O(bd) – the same as a simple minimax search. If the move ordering for the search is optimal (meaning the best moves are always searched first), the number of leaf node positions evaluated is about O(b*1*b*1*...*b) for odd depth and O(b*1*b*1*...*1) for even depth, or
. In the latter case, where the ply of a search is even, the effective branching factor is reduced to its square rootSquare root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
, or, equivalently, the search can go twice as deep with the same amount of computation. The explanation of b*1*b*1*... is that all the first player's moves must be studied to find the best one, but for each, only the best second player's move is needed to refute all but the first (and best) first player move – alpha-beta ensures no other second player moves need be considered.
Iterative deepening depth-first search
Iterative deepening depth-first search is a state space search strategy in which a depth-limited search is run repeatedly, increasing the depth limit with each iteration until it reaches d, the depth of the shallowest goal state...
.
The algorithm maintains two values, alpha and beta, which represent the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of respectively. Initially alpha is negative infinity and beta is positive infinity. As the recursion progresses the "window" becomes smaller. When beta becomes less than alpha, it means that the current position cannot be the result of best play by both players and hence need not be explored further.
Additionally, this algorithm can be trivially modified to return an entire principal variation in addition to the score. Some more aggressive algorithms such as MTD(f) do not easily permit such a modification.
Pseudocode
function alphabeta(node, depth, α, β, Player)if depth = 0 or node is a terminal node
return the heuristic value of node
if Player = MaxPlayer
for each child of node
α := max(α, alphabeta(child, depth-1, α, β, not(Player) ))
if β ≤ α
break (* Beta cut-off *)
return α
else
for each child of node
β := min(β, alphabeta(child, depth-1, α, β, not(Player) ))
if β ≤ α
break (* Alpha cut-off *)
return β
(* Initial call *)
alphabeta(origin, depth, -infinity, +infinity, MaxPlayer)
Heuristic improvements
Further improvement can be achieved without sacrificing accuracy, by using ordering heuristicHeuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
s to search parts of the tree that are likely to force alpha-beta cutoffs early. For example, in chess, moves that take pieces may be examined before moves that do not, or moves that have scored highly in earlier passes
Iterative deepening depth-first search
Iterative deepening depth-first search is a state space search strategy in which a depth-limited search is run repeatedly, increasing the depth limit with each iteration until it reaches d, the depth of the shallowest goal state...
through the game-tree analysis may be evaluated before others. Another common, and very cheap, heuristic is the killer heuristic
Killer heuristic
In competitive two-player games, the killer heuristic is a technique for improving the efficiency of alpha-beta pruning, which in turn improves the efficiency of the minimax algorithm. This algorithm has an exponential search time to find the optimal next move, so general methods for speeding it...
, where the last move that caused a beta-cutoff at the same level in the tree search is always examined first. This idea can be generalized into a set of refutation tables.
Alpha-beta search can be made even faster by considering only a narrow search window (generally determined by guesswork based on experience). This is known as aspiration search. In the extreme case, the search is performed with alpha and beta equal; a technique known as zero-window search, null-window search, or scout search. This is particularly useful for win/loss searches near the end of a game where the extra depth gained from the narrow window and a simple win/loss evaluation function may lead to a conclusive result. If an aspiration search fails, it is straightforward to detect whether it failed high (high edge of window was too low) or low (lower edge of window was too high). This gives information about what window values might be useful in a re-search of the position.
Other algorithms
More advanced algorithms that are even faster while still being able to compute the exact minimax value are known, such as NegascoutNegascout
NegaScout or Principal Variation Search is a negamax algorithm that can be faster than alpha-beta pruning. Like alpha-beta pruning, NegaScout is a directional search algorithm for computing the minimax value of a node in a tree...
and MTD-f
MTD-f
MTD, an abbreviation of MTD is a minimax search algorithm, an alternative to the alpha-beta pruning algorithm.- Zero Window Searches :...
.
Since the minimax algorithm and its variants are inherently depth-first
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
, a strategy such as iterative deepening
Iterative deepening depth-first search
Iterative deepening depth-first search is a state space search strategy in which a depth-limited search is run repeatedly, increasing the depth limit with each iteration until it reaches d, the depth of the shallowest goal state...
is usually used in conjunction with alpha-beta so that a reasonably good move can be returned even if the algorithm is interrupted before it has finished execution. Another advantage of using iterative deepening is that searches at shallower depths give move-ordering hints that can help produce cutoffs for higher depth searches much earlier than would otherwise be possible.
Algorithms like SSS*, on the other hand, use the best-first strategy. This can potentially make them more time-efficient, but typically at a heavy cost in space-efficiency.
See also
- Pruning (algorithm)Pruning (algorithm)Pruning is a technique in machine learning that reduces the size of decision trees by removing sections of the tree that provide little power to classify instances...
- Branch and boundBranch and boundBranch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
- MinimaxMinimaxMinimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
- Combinatorial optimizationCombinatorial optimizationIn applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
- NegamaxNegamaxNegamax search is a slightly variant formulation of minimax search that relies on the zero-sum property of a two-player game.This algorithm heavily relies on the fact that max = -min to simplify the implementation of the minimax algorithm. More precisely, the value of a position to player A in such...
- Transposition tableTransposition tableIn computer chess and other computer games, transposition tables are used to speed up the search of the game tree. Transposition tables are primarily useful in perfect information games, meaning the entire state of the game is known to all players at all times....
External links
- http://www.emunix.emich.edu/~evett/AI/AlphaBeta_movie/sld001.htm
- http://sern.ucalgary.ca/courses/CPSC/533/W99/presentations/L1_5B_McCullough_Melnyk/
- http://sern.ucalgary.ca/courses/CPSC/533/W99/presentations/L2_5B_Lima_Neitz/search.html
- http://www.maths.nott.ac.uk/personal/anw/G13GAM/alphabet.html
- http://chess.verhelst.org/search.html
- http://www.frayn.net/beowulf/index.html
- http://hal.inria.fr/docs/00/12/15/16/PDF/RR-6062.pdf
- Minimax (with or without alpha-beta pruning) algorithm visualization - game tree solving (Java Applet)
- Demonstration/animation of minimax game search algorithm with alpha-beta pruning (using html5, canvas, javascript, css)