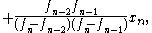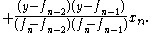Inverse quadratic interpolation
Encyclopedia
In numerical analysis
, inverse quadratic interpolation is a root-finding algorithm
, meaning that it is an algorithm for solving equations of the form f(x) = 0. The idea is to use quadratic interpolation
to approximate the inverse
of f. This algorithm is rarely used on its own, but it is important because it forms part of the popular Brent's method
.
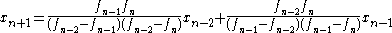
where fk = f(xk). As can be seen from the recurrence relation, this method requires three initial values, x0, x1 and x2.
to do quadratic interpolation on the inverse of f yields
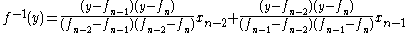
We are looking for a root of f, so we substitute y = f(x) = 0 in the above equation and this results in the above recursion formula.
The order of this convergence is approximately 1.8, it can be proved by the Secant Method analysis.
.
Inverse quadratic interpolation is also closely related to some other root-finding methods.
Using linear interpolation
instead of quadratic interpolation gives the secant method
. Interpolating f instead of the inverse of f gives Müller's method
.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, inverse quadratic interpolation is a root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
, meaning that it is an algorithm for solving equations of the form f(x) = 0. The idea is to use quadratic interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
to approximate the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of f. This algorithm is rarely used on its own, but it is important because it forms part of the popular Brent's method
Brent's method
In numerical analysis, Brent's method is a complicated but popular root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less reliable methods...
.
The method
The inverse quadratic interpolation algorithm is defined by the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
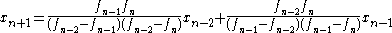
where fk = f(xk). As can be seen from the recurrence relation, this method requires three initial values, x0, x1 and x2.
Explanation of the method
We use the three preceding iterates, xn−2, xn−1 and xn, with their function values, fn−2, fn−1 and fn. Applying the Lagrange interpolation formulaLagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
to do quadratic interpolation on the inverse of f yields
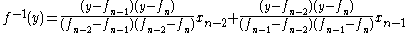
We are looking for a root of f, so we substitute y = f(x) = 0 in the above equation and this results in the above recursion formula.
Behaviour
The asymptotic behaviour is very good: generally, the iterates xn converge fast to the root once they get close. However, performance is often quite poor if you do not start very close to the actual root. For instance, if by any chance two of the function values fn−2, fn−1 and fn coincide, the algorithm fails completely. Thus, inverse quadratic interpolation is seldom used as a stand-alone algorithm.The order of this convergence is approximately 1.8, it can be proved by the Secant Method analysis.
Comparison with other root-finding methods
As noted in the introduction, inverse quadratic interpolation is used in Brent's methodBrent's method
In numerical analysis, Brent's method is a complicated but popular root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less reliable methods...
.
Inverse quadratic interpolation is also closely related to some other root-finding methods.
Using linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
instead of quadratic interpolation gives the secant method
Secant method
In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed...
. Interpolating f instead of the inverse of f gives Müller's method
Müller's method
Müller's method is a root-finding algorithm, a numerical method for solving equations of the form f = 0. It is first presented by D. E. Müller in 1956....
.
See also
- Successive parabolic interpolationSuccessive parabolic interpolationSuccessive parabolic interpolation is a technique for finding the extremum of a continuous unimodal function by successively fitting parabolas to the function at three unique points, and at each iteration replacing the "oldest" point with the extremum of the fitted parabola.- Advantages :Only...
is a related method that uses parabolas to find extrema rather than roots.