
Invariant factor
Encyclopedia
The invariant factors of a module
over a principal ideal domain
occur in one form of the structure theorem for finitely generated modules over a principal ideal domain
.
If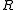 is a PID
is a PID
and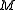 a finitely generated
a finitely generated 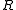 -module, then
-module, then
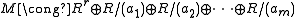
for some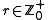 and nonzero elements
and nonzero elements 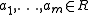 for which
for which 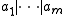 . The nonnegative integer
. The nonnegative integer  is called the free rank or Betti number of the module
is called the free rank or Betti number of the module 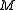 , while
, while 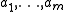 are the invariant factors of
are the invariant factors of 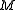 and are unique up to associatedness.
and are unique up to associatedness.
The invariant factors of a matrix
over a PID occur in the Smith normal form
and provide a means of computing the structure of a module from a set of generators and relations.
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
occur in one form of the structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
.
If
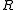 is a PID
is a PIDPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
and
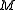 a finitely generated
a finitely generated 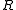 -module, then
-module, then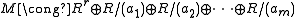
for some
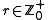 and nonzero elements
and nonzero elements 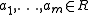 for which
for which 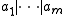 . The nonnegative integer
. The nonnegative integer  is called the free rank or Betti number of the module
is called the free rank or Betti number of the module 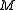 , while
, while 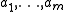 are the invariant factors of
are the invariant factors of 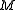 and are unique up to associatedness.
and are unique up to associatedness.The invariant factors of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over a PID occur in the Smith normal form
Smith normal form
In mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain . The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices...
and provide a means of computing the structure of a module from a set of generators and relations.

