
Information algebra
Encyclopedia
Classical information theory
goes back to Claude Shannon. It is a theory of information transmission, looking at communication and storage. However, it has not been considered so far that information comes from different sources and that it is therefore usually combined. It has furthermore been neglected in classical information theory that one wants to extract those parts out of a piece of information that are relevant to specific questions.
A mathematical phrasing of these operations leads to an algebra of information, describing basic modes of information processing. Such an algebra grasps a lot of formalisms of computer science
, which seem to be different on the surface: relational databases, multiple systems of formal logic or numerical problems of linear algebra. It allows the development of generic procedures of information processing and thus a unification of basic methods of computer science, in particular of distributed information processing.
 , where
, where 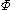 is a semigroup
is a semigroup
, representing combination or aggregation of information,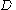 is a lattice
is a lattice
of domain
s (related to questions) whose partial order reflects the granularity of the domain or the question, and a mixed operation representing focusing or extraction of information.
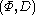 , the following operations are defined
, the following operations are defined
Additionally, in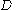 the usual lattice operations (meet and join) are defined.
the usual lattice operations (meet and join) are defined.
 , in addition to the axioms of the lattice
, in addition to the axioms of the lattice 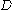 :
:
A two-sorted algebra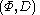 satisfying these axioms is called an Information Algebra.
satisfying these axioms is called an Information Algebra.
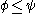 if
if 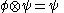 . This means that
. This means that 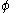 is less informative than
is less informative than 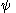 if it adds no new information to
if it adds no new information to  . The semigroup
. The semigroup 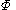 is a semilattice relative to this order, i.e.
is a semilattice relative to this order, i.e. 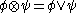 . Relative to any domain (question)
. Relative to any domain (question) 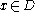 a partial order can be introduced by defining
a partial order can be introduced by defining 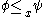 if
if 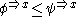 . It represents the order of information content of
. It represents the order of information content of 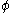 and
and 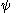 relative to the domain (question)
relative to the domain (question) 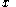 .
.
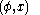 , where
, where 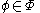 and
and  such that
such that 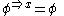 form a labeled Information Algebra. More precisely, in the two-sorted algebra
form a labeled Information Algebra. More precisely, in the two-sorted algebra  , the following operations are defined
, the following operations are defined
 be a set of symbols, called attributes (or column
be a set of symbols, called attributes (or column
names). For each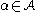 let
let 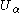 be a non-empty set, the
be a non-empty set, the
set of all possible values of the attribute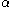 . For example, if
. For example, if
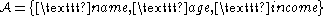 , then
, then 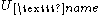 could
could
be the set of strings, whereas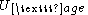 and
and 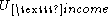 are both
are both
the set of non-negative integers.
Let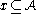 . An
. An 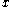 -tuple is a function
-tuple is a function 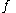 so that
so that
 and
and 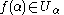 for each
for each 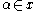 The set
The set
of all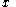 -tuples is denoted by
-tuples is denoted by 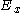 . For an
. For an 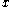 -tuple
-tuple 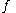 and a subset
and a subset
 the restriction
the restriction 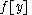 is defined to be the
is defined to be the
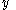 -tuple
-tuple 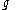 so that
so that 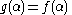 for all
for all 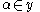 .
.
A relation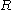 over
over 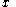 is a set of
is a set of  -tuples, i.e. a subset of
-tuples, i.e. a subset of 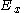 .
.
The set of attributes is called the domain of
is called the domain of 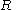 and denoted by
and denoted by
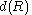 . For
. For 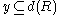 the projection of
the projection of 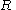 onto
onto 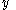 is defined
is defined
as follows:
The join of a relation over
over  and a relation
and a relation 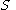 over
over 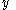 is
is
defined as follows: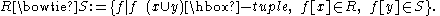
As an example, let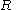 and
and  be the following relations:
be the following relations:
Then the join of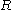 and
and 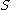 is:
is: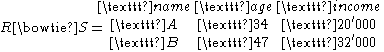
A relational database with natural join as combination and the usual projection
as combination and the usual projection 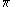 is an information algebra.
is an information algebra.
The operations are well defined since
It is easy to see that relational databases satisfy the axioms of a labeled
information algebra:
semigroup :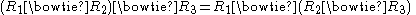 and
and 
transitivity : If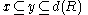 , then
, then 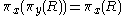 .
.
combination : If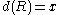 and
and 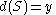 , then
, then  .
.
idempotency : If , then
, then 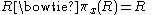 .
.
support : If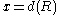 , then
, then 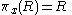 .
.
Domains and information systems: Compact Information Algebras are related to Scott domains and Scott information systems ;;.
Uncertain information : Random variables with values in information algebras represent probabilistic argumentation systems .
Semantic information : Information algebras introduce semantics by relating information to questions through focusing and combination ;.
Information flow : Information algebras are related to information flow, in particular classifications .
Tree decomposition : ...
Semigroup theory : ...
the axiom system proposed in (Shenoy and Shafer, 1990), see also (Shafer, 1991).
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
goes back to Claude Shannon. It is a theory of information transmission, looking at communication and storage. However, it has not been considered so far that information comes from different sources and that it is therefore usually combined. It has furthermore been neglected in classical information theory that one wants to extract those parts out of a piece of information that are relevant to specific questions.
A mathematical phrasing of these operations leads to an algebra of information, describing basic modes of information processing. Such an algebra grasps a lot of formalisms of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, which seem to be different on the surface: relational databases, multiple systems of formal logic or numerical problems of linear algebra. It allows the development of generic procedures of information processing and thus a unification of basic methods of computer science, in particular of distributed information processing.
Information algebra
Information relates to precise questions, comes from different sources, must be aggregated and can be focused on questions of interest. Starting from these considerations, information algebras are two-sorted algebras , where
, where 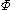 is a semigroup
is a semigroupSemigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, representing combination or aggregation of information,
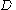 is a lattice
is a latticeLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
s (related to questions) whose partial order reflects the granularity of the domain or the question, and a mixed operation representing focusing or extraction of information.
Information and its operations
More precisely, in the two-sorted algebra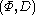 , the following operations are defined
, the following operations are definedCombination : 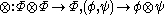 Focusing :  |
Additionally, in
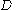 the usual lattice operations (meet and join) are defined.
the usual lattice operations (meet and join) are defined.Axioms and definition
The axioms of the two-sorted algebra , in addition to the axioms of the lattice
, in addition to the axioms of the lattice 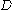 :
:Semigroup : 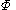 is a commutative semigroup under combination with a neutral element (representing vacuous information). is a commutative semigroup under combination with a neutral element (representing vacuous information).Distributivity of Focusing over Combination :  To focus an information on  combined with another information to domain combined with another information to domain 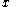 , one may as well first focus the second information to , one may as well first focus the second information to 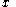 and combine then. and combine then.Transitivity of Focusing : 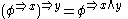 To focus an information on 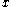 and and 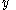 , one may focus it to , one may focus it to 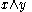 . .Idempotency :  An information combined with a part of itself gives nothing new. Support : 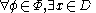 such that such that 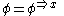 Each information refers to at least one domain (question). |
A two-sorted algebra
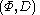 satisfying these axioms is called an Information Algebra.
satisfying these axioms is called an Information Algebra.Order of information
A partial order of information can be introduced by defining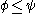 if
if 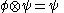 . This means that
. This means that 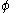 is less informative than
is less informative than 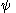 if it adds no new information to
if it adds no new information to  . The semigroup
. The semigroup 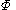 is a semilattice relative to this order, i.e.
is a semilattice relative to this order, i.e. 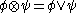 . Relative to any domain (question)
. Relative to any domain (question) 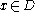 a partial order can be introduced by defining
a partial order can be introduced by defining 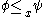 if
if 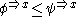 . It represents the order of information content of
. It represents the order of information content of 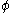 and
and 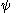 relative to the domain (question)
relative to the domain (question) 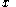 .
.Labeled information algebra
The pairs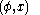 , where
, where 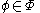 and
and  such that
such that 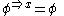 form a labeled Information Algebra. More precisely, in the two-sorted algebra
form a labeled Information Algebra. More precisely, in the two-sorted algebra  , the following operations are defined
, the following operations are defined
Labeling : 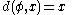 Combination : 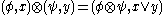 Projection : 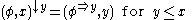 |
Models of information algebras
Here follows an incomplete list of instances of information algebras:- Relational algebraRelational algebraRelational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
: The reduct of a relational algebra with natural join as combination and the usual projection is a labeled information algebra, see Example. - Constraint systems: Constraints form an information algebra .
- Semiring valued algebras: C-Semirings induce information algebras ;;.
- LogicLogicIn philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
: Many logic systems induce information algebras . Reducts of cylindric algebraCylindric algebraThe notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Indeed, cylindric algebras are Boolean algebras equipped with additional...
s or polyadic algebraPolyadic algebraPolyadic algebras are algebraic structures introduced by Paul Halmos. They are related to first-order logic in a way analogous to the relationship between Boolean algebras and propositional logic .There are other ways to relate first-order logic to algebra, including Tarski's cylindric algebras...
s are information algebras related to predicate logicPredicate logicIn mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
. - Module algebraModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s: ;. - Linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s: Systems of linear equations or linear inequalities induce information algebras .
Worked-out example: relational algebra
Let be a set of symbols, called attributes (or column
be a set of symbols, called attributes (or columnnames). For each
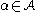 let
let 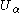 be a non-empty set, the
be a non-empty set, theset of all possible values of the attribute
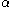 . For example, if
. For example, if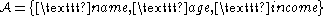 , then
, then 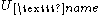 could
couldbe the set of strings, whereas
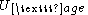 and
and 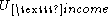 are both
are boththe set of non-negative integers.
Let
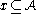 . An
. An 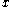 -tuple is a function
-tuple is a function 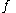 so that
so that and
and 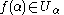 for each
for each 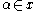 The set
The setof all
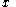 -tuples is denoted by
-tuples is denoted by 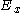 . For an
. For an 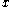 -tuple
-tuple 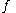 and a subset
and a subset the restriction
the restriction 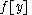 is defined to be the
is defined to be the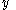 -tuple
-tuple 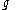 so that
so that 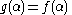 for all
for all 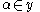 .
.A relation
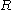 over
over 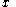 is a set of
is a set of  -tuples, i.e. a subset of
-tuples, i.e. a subset of 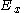 .
.The set of attributes
 is called the domain of
is called the domain of 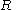 and denoted by
and denoted by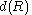 . For
. For 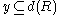 the projection of
the projection of 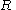 onto
onto 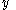 is defined
is definedas follows:

The join of a relation
 over
over  and a relation
and a relation 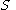 over
over 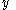 is
isdefined as follows:
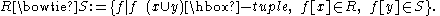
As an example, let
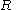 and
and  be the following relations:
be the following relations:
Then the join of
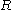 and
and 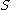 is:
is: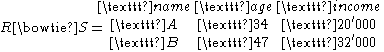
A relational database with natural join
 as combination and the usual projection
as combination and the usual projection 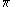 is an information algebra.
is an information algebra.The operations are well defined since
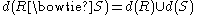
- If
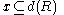 , then
, then  .
.
It is easy to see that relational databases satisfy the axioms of a labeled
information algebra:
semigroup :
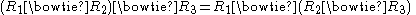 and
and 
transitivity : If
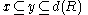 , then
, then 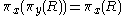 .
.combination : If
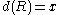 and
and 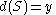 , then
, then  .
.idempotency : If
 , then
, then 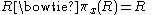 .
.support : If
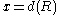 , then
, then 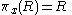 .
.Connections
Valuation algebras : Dropping the idempotency axiom leads to Valuation Algebras. These axioms have been introduced by to generalize local computation schemes from Bayesian networks to more general formalisms (including belief function, possibility potentials, etc.) .Domains and information systems: Compact Information Algebras are related to Scott domains and Scott information systems ;;.
Uncertain information : Random variables with values in information algebras represent probabilistic argumentation systems .
Semantic information : Information algebras introduce semantics by relating information to questions through focusing and combination ;.
Information flow : Information algebras are related to information flow, in particular classifications .
Tree decomposition : ...
Semigroup theory : ...
Historical Roots
The axioms for information algebras are derived fromthe axiom system proposed in (Shenoy and Shafer, 1990), see also (Shafer, 1991).

