Induced homomorphism (algebraic topology)
Encyclopedia
In mathematics
, especially in the area of topology
known as algebraic topology
, an induced homomorphism is a way of relating the algebraic invariants of topological space
s which are already related by a continuous function
. Such homomorphism exist whenever the algebraic invariants are functor
ial. For example, they exist for fundamental group
s, higher homotopy group
s, singular homology
, and De Rham cohomology
. For the more categorical
approach, see induced homomorphism
, and for the specific case of fundamental groups, see induced homomorphism (fundamental group)
.
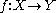between topological spaces (possibly with some additional structure) induces homomorphisms between various algebraic structures associated with 
and 
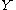, respectively.
. Likewise there are induced homomorphisms of higher homotopy group
s and homology groups.
Any homology theory
comes with induced homomorphisms. For instance, simplicial homology
, singular homology
, and Borel-Moore homology
all have induced homomorphisms. Similarly, any cohomology
comes induced homomorphisms. For instance, Čech cohomology
, de Rham cohomology
, and singular cohomology all have induced homomorphisms. Generalizations such as cobordism
also have induced homomorphisms.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
known as algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, an induced homomorphism is a way of relating the algebraic invariants of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s which are already related by a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Such homomorphism exist whenever the algebraic invariants are functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ial. For example, they exist for fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s, higher homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s, singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, and De Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. For the more categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
approach, see induced homomorphism
Induced homomorphism
In mathematics, an induced homomorphism is a structure-preserving map between a pair of objects that is derived in a canonical way from another map between another pair of objects. A particularly important case arises in algebraic topology, where any continuous function between two pointed...
, and for the specific case of fundamental groups, see induced homomorphism (fundamental group)
Induced homomorphism (fundamental group)
In mathematics, especially in the area of topology known as algebraic topology, the induced homomorphism is a group homomorphism related to the study of the fundamental group.-Definition:...
.
Definitions
A continuous function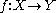 between topological spaces (possibly with some additional structure) induces homomorphisms between various algebraic structures associated with and 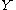, respectively.Examples
A useful example is the induced homomorphism of fundamental groupsInduced homomorphism (fundamental group)
In mathematics, especially in the area of topology known as algebraic topology, the induced homomorphism is a group homomorphism related to the study of the fundamental group.-Definition:...
. Likewise there are induced homomorphisms of higher homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s and homology groups.
Any homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
comes with induced homomorphisms. For instance, simplicial homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
, singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, and Borel-Moore homology
Borel-Moore homology
In mathematics, Borel−Moore homology or homology with closed support is a homology theory for locally compact spaces, introduced by .For compact spaces, the Borel−Moore homology coincide with the usual singular homology, but for non-compact spaces, it usually gives homology groups with better...
all have induced homomorphisms. Similarly, any cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
comes induced homomorphisms. For instance, Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
, de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
, and singular cohomology all have induced homomorphisms. Generalizations such as cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
also have induced homomorphisms.