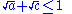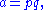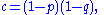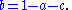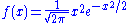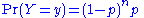Indecomposable

• The simplest examples are Bernoulli distributions: if

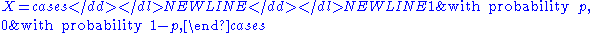
then the probability distribution of X is indecomposable.

Proof: Given non-constant distributions U and V, so that U assumes at least two values a, b and V assumes two values c, d, with a < b and c < d, then U + V assumes at least three distinct values: a + c, a + d, b + d (b + c may be equal to a + d, for example if one uses 0, 1 and 0, 1). Thus the sum of non-constant distributions assumes at least three values, so the Bernoulli distribution is not the sum of non-constant distributions.

• Suppose a + b + c = 1, a, b, c ≥ 0, and

This probability distribution is decomposable (as the sum of two Bernoulli distributions) if

and otherwise indecomposable. To see, this, suppose U and V are independent random variables and U + V has this probability distribution. Then we must have

for some p, q ∈ [0, 1], by similar reasoning to the Bernoulli case (otherwise the sum U + V will assume more than three values). It follows that

This system of two quadratic equations in two variables p and q has a solution (p, q) ∈ [0, 1]² if and only if

Thus, for example, the discrete uniform distribution on the set {0, 1, 2} is indecomposable, but the binomial distribution assigning respective probabilities 1/4, 1/2, 1/4 is decomposable.

• An absolutely continuous
  Absolute continuity
  In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
  
   indecomposable distribution. It can be shown that the distribution whose density function
  Probability density function
  In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
  
   is

is indecomposable.

Decomposable

• All infinitely divisible
  Infinite divisibility (probability)
  The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
  
   distributions are a fortiori decomposable; in particular, this includes the stable distributions, such as the normal distribution.

• The uniform distribution
  Uniform distribution (continuous)
  In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
  
   on the interval [0, 1] is decomposable, since it is the sum of the Bernoulli variable that assumes 0 or 1/2 with equal probabilities and the uniform distribution on [0, 1/2]. Iterating this yields the infinite decomposition:

where the independent random variables X_n are each equal to 0 or 1 with equal probabilities – this is a Bernoulli trial of each digit of the binary expansion.

• A sum of indecomposable random variables is necessarily decomposable (as it is a sum), and in fact may a fortiori be an infinitely divisible distribution (not just decomposable as the given sum). Suppose a random variable Y has a geometric distribution

on {0, 1, 2, ...}. For any positive integer k, there is a sequence of negative-binomially distributed

Negative binomial distribution

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...

 random variables Y_j, j = 1, ..., k, such that Y₁ + ... + Y_k has this geometric distribution. Therefore, this distribution is infinitely divisible. But now let D_n be the nth binary digit of Y, for n ≥ 0. Then the Ds are independent and

and each term in this sum is indecomposable.

Related concepts

At the other extreme from indecomposability is infinite divisibility

Infinite divisibility (probability)

The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...

.

• Cramér's theorem
  Cramér's theorem
  In mathematical statistics, Cramér's theorem is one of several theorems of Harald Cramér, a Swedish statistician and probabilist.- Normal random variables :...
  
   shows that while the normal distribution is infinitely divisible, it can only be decomposed into normal distributions.
• Cochran's theorem
  Cochran's theorem
  In statistics, Cochran's theorem, devised by William G. Cochran, is a theorem used in to justify results relating to the probability distributions of statistics that are used in the analysis of variance.- Statement :...
  
   shows that decompositions of a sum of squares of normal random variables into sums of squares of linear combinations of these variables are always independent chi-squared distributions.

See also

• Cramér's theorem
  Cramér's theorem
  In mathematical statistics, Cramér's theorem is one of several theorems of Harald Cramér, a Swedish statistician and probabilist.- Normal random variables :...
  
  
• Cochran's theorem
  Cochran's theorem
  In statistics, Cochran's theorem, devised by William G. Cochran, is a theorem used in to justify results relating to the probability distributions of statistics that are used in the analysis of variance.- Statement :...
  
  
• Infinite divisibility (probability)
  Infinite divisibility (probability)
  The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
  
  

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.