Padding argument
Encyclopedia
In computational complexity theory
, the padding argument is a tool to conditionally prove that if some complexity classes are equal, then some other bigger classes are also equal.
is equal to NP
then EXP
is equal to NEXP. Indeed, let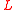
a language in NEXP, in time 
, then 
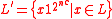where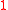 
is a new symbol and 
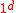means that 
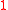is written 
times, is a language computed in non deterministic polynomial time, since it can check if there is enough 1 by computing 
, reject if it has not enough time to do this computation, and if there is enough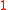 
it can simulate the computation in 
time of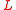 
. By the assumption that P = NP there is also a deterministic algorithm accepting 
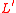, which means that writing 2nc 1 and then simulating this new algorithm would be a correct algorithm to decide L in exponential time.
The 1d is called the padding of the language L. In some case, this argument can be used for space complexity classes, for alternating classes and for bounded alternating classes.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the padding argument is a tool to conditionally prove that if some complexity classes are equal, then some other bigger classes are also equal.
Example
If P (complexity)P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
is equal to NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
then EXP
Exp
Exp may stand for:* Exponential function, in mathematics* Expiry date of organic compounds like food or medicines* Experience points, in role-playing games* EXPTIME, a complexity class in computing* Ford EXP, a car manufactured in the 1980s...
is equal to NEXP. Indeed, let
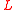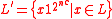a language in NEXP, in time , then where 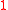is a new symbol and 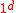means that 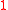is written times, is a language computed in non deterministic polynomial time, since it can check if there is enough 1 by computing , reject if it has not enough time to do this computation, and if there is enough 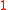it can simulate the computation in time of 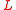. By the assumption that P = NP there is also a deterministic algorithm accepting 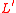, which means that writing 2nc 1 and then simulating this new algorithm would be a correct algorithm to decide L in exponential time.The 1d is called the padding of the language L. In some case, this argument can be used for space complexity classes, for alternating classes and for bounded alternating classes.