Idealized greenhouse model
Encyclopedia
The surface of the sun
radiates light and heat
at approximately 5,500 °C. The earth
is much cooler and so radiates heat back away from itself at much longer wavelengths, mostly in the infrared
range. The idealized greenhouse model is based on the fact that certain gases in the Earth's atmosphere, including carbon dioxide
and water vapour, are transparent to the high-frequency, high-energy solar radiation, but are much more opaque to the lower frequency infrared radiation leaving the surface of the earth. Thus heat is easily let in, but is partially trapped by these gases as it tries to leave. Rather than get hotter and hotter, Kirchhoff's law of thermal radiation
says that the gases of the atmosphere also have to re-emit the infrared energy that they absorb, and they do so, also at long infrared wavelengths, both upwards into space as well as downwards back towards the Earth's surface. In the long-term, thermal equilibrium is reached when all the heat energy arriving on the planet is leaving again at the same rate. In this idealized model, the greenhouse gases cause the surface of the planet to be warmer than it would be without them, in order for the required amount of heat energy finally to be radiated out into space from the top of the atmosphere.
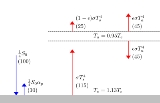
The greenhouse effect
can be illustrated with an idealized planet. This is a common "textbook model": the planet will have a constant surface temperature Ts and an atmosphere with constant temperature Ta. For diagrammatic clarity,
a gap can be depicted between the atmosphere and the surface. Alternatively, Ts could be
interpreted as a temperature representative of the surface and the lower atmosphere, and Ta
could be interpreted as the temperature of the upper atmosphere. In order to justify that Ta
and Ts remain constant over the planet, strong ocean and atmospheric currents can be imagined to provide plentiful
lateral mixing. Furthermore, any daily or seasonal cycles in temperature are assumed to be insignificant.
escaping the top of the atmosphere, to be equal to the absorbed radiative power of sunlight
.
When applied to a planet like Earth, the outgoing radiation will be longwave and the sunlight will be shortwave.
These two streams of radiation will have distinct emission and absorption characteristics. In the idealized model, we assume the atmosphere is
completely transparent to sunlight. The planetary albedo
αP is the fraction
of the incoming solar flux that is reflected back to space (since the atmosphere is assumed totally transparent to solar radiation, it does not matter whether this albedo is imagined to be caused by reflection at the surface of the planet or at the top of the atmosphere or a mixture). The flux density of the incoming solar radiation
is specified by the solar constant
S0. For application to planet Earth, appropriate values are
S0=1366 W m−2 and αP=0.30. Accounting for the fact that the surface area of a
sphere is 4 times the area of its intercept (its shadow), the average incoming radiation is
S0/4.
For longwave radiation, the surface of the Earth is assumed to have an emissivity of 1 (i.e., the earth is a black body in the infrared, which is realistic). The surface emits a radiative flux density F according to the Stefan-Boltzmann law:
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
radiates light and heat
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
at approximately 5,500 °C. The earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is much cooler and so radiates heat back away from itself at much longer wavelengths, mostly in the infrared
Infrared
Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm...
range. The idealized greenhouse model is based on the fact that certain gases in the Earth's atmosphere, including carbon dioxide
Carbon dioxide
Carbon dioxide is a naturally occurring chemical compound composed of two oxygen atoms covalently bonded to a single carbon atom...
and water vapour, are transparent to the high-frequency, high-energy solar radiation, but are much more opaque to the lower frequency infrared radiation leaving the surface of the earth. Thus heat is easily let in, but is partially trapped by these gases as it tries to leave. Rather than get hotter and hotter, Kirchhoff's law of thermal radiation
Kirchhoff's law of thermal radiation
In thermodynamics, Kirchhoff's law of thermal radiation, or Kirchhoff's law for short, is a general statement equating emission and absorption in heated objects, proposed by Gustav Kirchhoff in 1859, following from general considerations of thermodynamic equilibrium and detailed balance.An object...
says that the gases of the atmosphere also have to re-emit the infrared energy that they absorb, and they do so, also at long infrared wavelengths, both upwards into space as well as downwards back towards the Earth's surface. In the long-term, thermal equilibrium is reached when all the heat energy arriving on the planet is leaving again at the same rate. In this idealized model, the greenhouse gases cause the surface of the planet to be warmer than it would be without them, in order for the required amount of heat energy finally to be radiated out into space from the top of the atmosphere.
The greenhouse effect
Greenhouse effect
The greenhouse effect is a process by which thermal radiation from a planetary surface is absorbed by atmospheric greenhouse gases, and is re-radiated in all directions. Since part of this re-radiation is back towards the surface, energy is transferred to the surface and the lower atmosphere...
can be illustrated with an idealized planet. This is a common "textbook model": the planet will have a constant surface temperature Ts and an atmosphere with constant temperature Ta. For diagrammatic clarity,
a gap can be depicted between the atmosphere and the surface. Alternatively, Ts could be
interpreted as a temperature representative of the surface and the lower atmosphere, and Ta
could be interpreted as the temperature of the upper atmosphere. In order to justify that Ta
and Ts remain constant over the planet, strong ocean and atmospheric currents can be imagined to provide plentiful
lateral mixing. Furthermore, any daily or seasonal cycles in temperature are assumed to be insignificant.
The model
The model will find the values of Ts and Ta that will allow the outgoing radiative power,escaping the top of the atmosphere, to be equal to the absorbed radiative power of sunlight
Sunlight
Sunlight, in the broad sense, is the total frequency spectrum of electromagnetic radiation given off by the Sun. On Earth, sunlight is filtered through the Earth's atmosphere, and solar radiation is obvious as daylight when the Sun is above the horizon.When the direct solar radiation is not blocked...
.
When applied to a planet like Earth, the outgoing radiation will be longwave and the sunlight will be shortwave.
These two streams of radiation will have distinct emission and absorption characteristics. In the idealized model, we assume the atmosphere is
completely transparent to sunlight. The planetary albedo
Albedo
Albedo , or reflection coefficient, is the diffuse reflectivity or reflecting power of a surface. It is defined as the ratio of reflected radiation from the surface to incident radiation upon it...
αP is the fraction
of the incoming solar flux that is reflected back to space (since the atmosphere is assumed totally transparent to solar radiation, it does not matter whether this albedo is imagined to be caused by reflection at the surface of the planet or at the top of the atmosphere or a mixture). The flux density of the incoming solar radiation
is specified by the solar constant
Solar constant
The solar constant, a measure of flux density, is the amount of incoming solar electromagnetic radiation per unit area that would be incident on a plane perpendicular to the rays, at a distance of one astronomical unit...
S0. For application to planet Earth, appropriate values are
S0=1366 W m−2 and αP=0.30. Accounting for the fact that the surface area of a
sphere is 4 times the area of its intercept (its shadow), the average incoming radiation is
S0/4.
For longwave radiation, the surface of the Earth is assumed to have an emissivity of 1 (i.e., the earth is a black body in the infrared, which is realistic). The surface emits a radiative flux density F according to the Stefan-Boltzmann law:
-

where σ is the Stefan-Boltzmann constantStefan-Boltzmann constantThe Stefan–Boltzmann constant , a physical constant denoted by the Greek letter σ, is the constant of proportionality in the Stefan–Boltzmann law: the total energy radiated per unit surface area of a black body in unit time is proportional to the fourth power of the thermodynamic temperature.The...
. A key to understanding the greenhouse effect is Kirchhoff's law of thermal radiationKirchhoff's law of thermal radiationIn thermodynamics, Kirchhoff's law of thermal radiation, or Kirchhoff's law for short, is a general statement equating emission and absorption in heated objects, proposed by Gustav Kirchhoff in 1859, following from general considerations of thermodynamic equilibrium and detailed balance.An object...
. At any given wavelength the absorptivity of the atmosphere will be equal to the emissivity. Radiation from the surface
could be in a slightly different portion of the infrared spectrum than the radiation emitted by the atmosphere. The model assumes
that the average emissivity (absorptivity) is identical for either of these streams of infrared radiation, as they interact with the atmosphere. Thus, for longwave radiation, one symbol ε denotes both the emissivity and absorptivity of the atmosphere, for
any stream of infrared radiation.
 The infrared flux density out of the top of the atmosphere:
The infrared flux density out of the top of the atmosphere: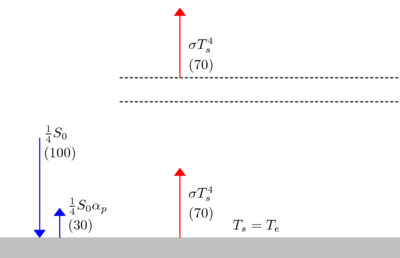
-

In the last term, ε represents the fraction of upward longwave radiation
from the surface that is absorbed, the absorptivity of the atmosphere.
In the first term on the right, ε is the emissivity of the atmosphere,
the adjustment of the Stefan-Boltzmann law to account for the fact that
the atmosphere is not optically thick. Thus ε plays the role of neatly blending,
or averaging, the two streams of
radiation in the calculation of the outward flux density.
Zero net radiation leaving the top of the atmosphere requires:-

Zero net radiation entering the surface requires:-

Energy equilibrium of the atmosphere can be either derived from the two above equilibrium conditions, or independently deduced:-

Note the important factor of 2, resulting from the fact that the atmosphere radiates both upward and downward.
Thus the ratio of Ta to Ts is independent of ε:-

Thus Ta can be expressed in terms of Ts, and a solution is obtained for
Ts in terms of the model input parameters:-

or-

The solution can also be expressed in terms of the effective emission temperatureEffective temperatureThe effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation...
Te,
which is the temperature that characterizes the outgoing infrared flux density F, as if the radiator
were a perfect radiator obeying F=σTe4. This is easy to conceptualize in the context of the
model. Te is also the solution for Ts, for the case of ε=0, or no atmosphere:-

With the definition of Te:-

For a perfect greenhouse, with no radiation escaping from the surface, or ε=1:-

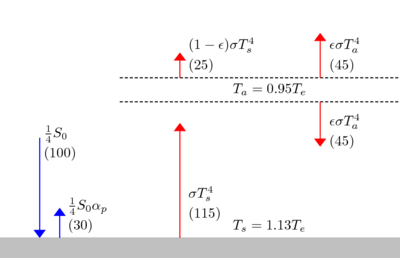
Using the parameters defined above to be appropriate for Earth,
For ε=1:
For ε=0.78,-
 .
.
This value of Ts happens to
be close to a very widely quoted (but unattributed) 288 K claimed for the average global "surface temperature". ε=0.78 implies 22% of the surface radiation escapes directly to space,
consistent with the statement of 15% to 30% escaping in the greenhouse effectGreenhouse effectThe greenhouse effect is a process by which thermal radiation from a planetary surface is absorbed by atmospheric greenhouse gases, and is re-radiated in all directions. Since part of this re-radiation is back towards the surface, energy is transferred to the surface and the lower atmosphere...
.
The radiative forcingRadiative forcingIn climate science, radiative forcing is generally defined as the change in net irradiance between different layers of the atmosphere. Typically, radiative forcing is quantified at the tropopause in units of watts per square meter. A positive forcing tends to warm the system, while a negative...
for doubling carbon dioxide is 3.71 W m−2, in a simple parameterization. This is also the value endorsed by the IPCCIntergovernmental Panel on Climate ChangeThe Intergovernmental Panel on Climate Change is a scientific intergovernmental body which provides comprehensive assessments of current scientific, technical and socio-economic information worldwide about the risk of climate change caused by human activity, its potential environmental and...
.
From the equation for ,
,
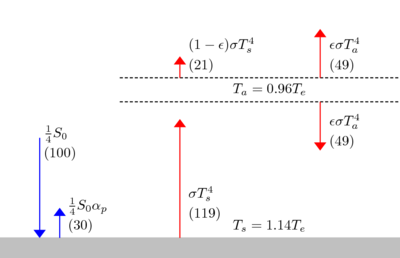
Using the values of Ts and Ta for ε=0.78 allows for = -3.71 W m−2 with Δε=.019. Thus a change of ε from 0.78 to 0.80 is consistent with the radiative forcing from
= -3.71 W m−2 with Δε=.019. Thus a change of ε from 0.78 to 0.80 is consistent with the radiative forcing from
a doubling of carbon dioxide. For ε=0.80,
Thus this model predicts a global warming of ΔTs = 1.2 K for a doubling of carbon dioxide. A typical prediction from a GCMGlobal climate modelA General Circulation Model is a mathematical model of the general circulation of a planetary atmosphere or ocean and based on the Navier–Stokes equations on a rotating sphere with thermodynamic terms for various energy sources . These equations are the basis for complex computer programs commonly...
is 3 K surface warming,
primarily because the GCM allows for positive feedback, notably from increased water vapor.
A simple surrogate for including this feedback process is to posit an additional increase of Δε=.02,
for a total Δε=.04, to approximate
the effect of the increase in water vapor that would be associated with an increase in temperature.
This idealized model then predicts a global warming of ΔTs = 2.4 K for a doubling of carbon dioxide, roughly consistent with the IPCC.
Extensions
The simple one-level atmospheric model can be readily extended to a multiple-layer atmosphere. In this case the equations for the temperatures become a series of coupled equations. This simple model always predicts a decreasing temperature away from the surface, and all levels increase in temperature as "greenhouse gases are added". Neither of these effects are fully realistic: in the real atmosphere temperatures increase above the tropopause, and temperatures in that layer are predicted (and observed) to decrease as GHG's are added. This is directly related to the non-greyness of the real atmosphere.
See also
- Greenhouse effectGreenhouse effectThe greenhouse effect is a process by which thermal radiation from a planetary surface is absorbed by atmospheric greenhouse gases, and is re-radiated in all directions. Since part of this re-radiation is back towards the surface, energy is transferred to the surface and the lower atmosphere...
- Anti-greenhouse effectAnti-Greenhouse EffectThe anti-greenhouse effect is a neologism used to describe two different effects that describe a cooling effect an atmosphere has on the ambient temperature of the planet. Unlike the greenhouse effect, which is common, an anti-greenhouse effect is only known to exist in one situation in our Solar...
- Climate changeClimate changeClimate change is a significant and lasting change in the statistical distribution of weather patterns over periods ranging from decades to millions of years. It may be a change in average weather conditions or the distribution of events around that average...
- Climate forcing
- Earth's energy budgetEarth's energy budgetThe Earth can be considered as a physical system with an energy budget that includes all gains of incoming energy and all losses of outgoing energy. The planet is approximately in equilibrium, so the sum of the gains is approximately equal to the sum of the losses.Note on accompanying images:...
- Earth's radiation balanceEarth's radiation balanceEarth's radiation balance is the equation of the incoming and outgoing thermal radiation.The incoming solar radiation is short wave, therefore the equation below is called the short wave radiation balance Qs:* G = global radiation...
- Global dimmingGlobal dimmingGlobal dimming is the gradual reduction in the amount of global direct irradiance at the Earth's surface that was observed for several decades after the start of systematic measurements in the 1950s. The effect varies by location, but worldwide it has been estimated to be of the order of a 4%...
- Global warmingGlobal warmingGlobal warming refers to the rising average temperature of Earth's atmosphere and oceans and its projected continuation. In the last 100 years, Earth's average surface temperature increased by about with about two thirds of the increase occurring over just the last three decades...
-
-
-
-
-
-
-
-
-
-
-





