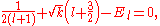Hooke's atom
Encyclopedia
Hooke's atom, also known as harmonium, refers to an artificial helium
-like atom where the Coulombic
electron-nucleus interaction potential is
replaced by a harmonic potential
. This system is of significance as it is, for certain values of the force constant defining the harmonic containment, an exactly solvable ground-state many-electron problem
that explicitly includes electron correlation
. As such it can provide insight in to quantum correlation (albeit in the presence of a non-physical nuclear potential) and can act as a test system for judging the accuracy of approximate quantum chemical methods
for solving the Schrödinger equation
. The name "Hooke's atom" arises because the harmonic potential used to describe the electron-nucleus interaction is a consequence of Hooke's law
.
, the Hamiltonian
defining the Hooke's atom is
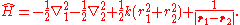
As written, the first two terms are the kinetic energy operators of the two electrons, the third term is the harmonic electron-nucleus potential, and the final term the electron-electron interaction potential. The non-relativistic Hamiltonian of the helium atom differs only in the replacement:
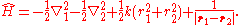
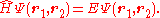
For arbitrary values of the force constant, k, the Schrödinger equation does not have an analytic solution. However, for a countably infinite
number of values, such as k=¼, simple closed form solutions can be derived. Given the artificial nature of the system this restriction does not hinder the usefulness of the solution.
To solve, the system is first transformed form the Cartesian electronic coordinates, (r1,r2), to the center of mass coordinates, (R,u), defined as
Under this transformation, the Hamiltonian becomes separable – that is, the |r1 - r2| term coupling the two electrons is removed (and not replaced by some other form) allowing the general separation of variables
technique to be applied to further a solution for the wave function in the form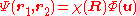
. The original Schrödinger equation is then replaced by:
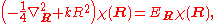
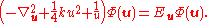
The first equation for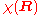
is the Schrödinger equation for an isotropic quantum harmonic oscillator with ground-state energy 
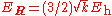and (unnormalized) wave function
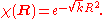
Asymptotically, the second equation again behaves as a harmonic oscillator of the form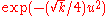
and the rotationally invariant ground state can be expressed, in general, as 
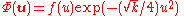for some function 
. It was long noted that f(u) is very well approximated by a linear function in u. Thirty years after the proposal of the model an exact solution was discovered for k=¼, and it was seen that f(u)=1+u/2. It was latter shown that there are many values of k which lead to an exact solution for the ground state, as will be shown in the following.
Decomposing
and expressing the Laplacian in spherical coordinates,
one further decomposes the radial wave function as
which removes the first derivative to yield
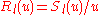
The asymptotic behavior
encourages a solution of the form
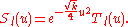
The differential equation satisfied by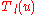
is
This equation lends itself to a solution by way of the Frobenius method
. That is,
is expressed as
for some
and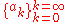 
which satisfy:
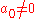
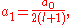
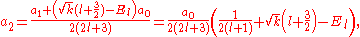
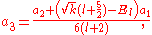
The two solutions to the indicial equation are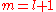
and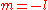 
of which the former is taken as it yields the regular (bounded, normalizable) wave function. For a simple solution to exist, the infinite series is sought to terminate and it is here where particular values of k are exploited for an exact closed-form solution. Terminating the polynomial at any particular order can be accomplished with different values of k defining the Hamiltonian. As such there exists an infinite number of systems, differing only in the strength of the harmonic containment, with exact ground-state solutions. Most simply, to impose ak = 0 for k ≥ 2, two conditions must be satisfied:
These directly force a2 = 0 and a3 = 0 respectively, and as a consequence of the three term recession, all higher coefficients also vanish. Solving for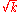
and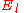 
yields
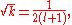
and the radial wave function
Transforming back to
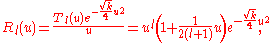
the ground-state (with
and energy 
) is finally
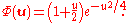
Combing, normalizing, and transforming back to the original coordinates yields the ground state wave function:
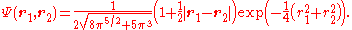
of the Hooke atom is
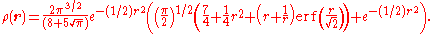
From this we see that the radial derivative of the density vanishes at the nucleus. This is in stark contrast to the real (non-relativistic) helium atom where the density displays a cusp at the nucleus as a result of the unbounded Coulomb potential.
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
-like atom where the Coulombic
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
electron-nucleus interaction potential is
replaced by a harmonic potential
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
. This system is of significance as it is, for certain values of the force constant defining the harmonic containment, an exactly solvable ground-state many-electron problem
Many-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
that explicitly includes electron correlation
Electronic correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system.- Atomic and molecular systems :...
. As such it can provide insight in to quantum correlation (albeit in the presence of a non-physical nuclear potential) and can act as a test system for judging the accuracy of approximate quantum chemical methods
Computational chemistry
Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...
for solving the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. The name "Hooke's atom" arises because the harmonic potential used to describe the electron-nucleus interaction is a consequence of Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
.
Definition
Employing atomic unitsAtomic units
Atomic units form a system of natural units which is especially convenient for atomic physics calculations. There are two different kinds of atomic units, which one might name Hartree atomic units and Rydberg atomic units, which differ in the choice of the unit of mass and charge. This article...
, the Hamiltonian
Molecular Hamiltonian
In atomic, molecular, and optical physics as well as in quantum chemistry, molecular Hamiltonian is the name given to the Hamiltonian representing the energy of the electrons and nuclei in a molecule...
defining the Hooke's atom is
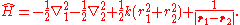
As written, the first two terms are the kinetic energy operators of the two electrons, the third term is the harmonic electron-nucleus potential, and the final term the electron-electron interaction potential. The non-relativistic Hamiltonian of the helium atom differs only in the replacement:
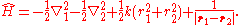
Solution
The equation to be solved is the two electron Schrödinger equation: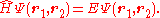For arbitrary values of the force constant, k, the Schrödinger equation does not have an analytic solution. However, for a countably infinite
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
number of values, such as k=¼, simple closed form solutions can be derived. Given the artificial nature of the system this restriction does not hinder the usefulness of the solution.
To solve, the system is first transformed form the Cartesian electronic coordinates, (r1,r2), to the center of mass coordinates, (R,u), defined as
Under this transformation, the Hamiltonian becomes separable – that is, the |r1 - r2| term coupling the two electrons is removed (and not replaced by some other form) allowing the general separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
technique to be applied to further a solution for the wave function in the form
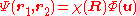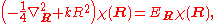
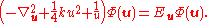
. The original Schrödinger equation is then replaced by:The first equation for
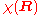is the Schrödinger equation for an isotropic quantum harmonic oscillator with ground-state energy 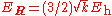and (unnormalized) wave function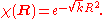Asymptotically, the second equation again behaves as a harmonic oscillator of the form
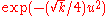and the rotationally invariant ground state can be expressed, in general, as 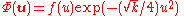for some function . It was long noted that f(u) is very well approximated by a linear function in u. Thirty years after the proposal of the model an exact solution was discovered for k=¼, and it was seen that f(u)=1+u/2. It was latter shown that there are many values of k which lead to an exact solution for the ground state, as will be shown in the following.Decomposing
and expressing the Laplacian in spherical coordinates,one further decomposes the radial wave function as
which removes the first derivative to yield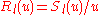The asymptotic behavior
encourages a solution of the form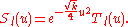The differential equation satisfied by
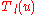isThis equation lends itself to a solution by way of the Frobenius method
Frobenius method
In mathematics, the Frobenius method, named after Ferdinand Georg Frobenius, is a way to find an infinite series solution for a second-order ordinary differential equation of the formin the vicinity of the regular singular point z=0....
. That is,
is expressed asfor some
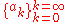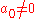
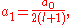
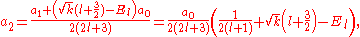
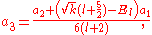
and which satisfy:The two solutions to the indicial equation are
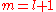and 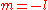of which the former is taken as it yields the regular (bounded, normalizable) wave function. For a simple solution to exist, the infinite series is sought to terminate and it is here where particular values of k are exploited for an exact closed-form solution. Terminating the polynomial at any particular order can be accomplished with different values of k defining the Hamiltonian. As such there exists an infinite number of systems, differing only in the strength of the harmonic containment, with exact ground-state solutions. Most simply, to impose ak = 0 for k ≥ 2, two conditions must be satisfied:
These directly force a2 = 0 and a3 = 0 respectively, and as a consequence of the three term recession, all higher coefficients also vanish. Solving for
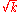and 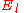yields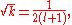and the radial wave function
Transforming back to
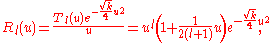
the ground-state (with
and energy ) is finally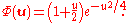Combing, normalizing, and transforming back to the original coordinates yields the ground state wave function:
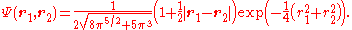
Remarks
The exact ground state electronic densityElectronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
of the Hooke atom is
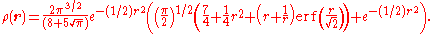
From this we see that the radial derivative of the density vanishes at the nucleus. This is in stark contrast to the real (non-relativistic) helium atom where the density displays a cusp at the nucleus as a result of the unbounded Coulomb potential.