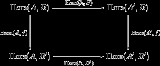
Hom functor
Encyclopedia
In mathematics
, specifically in category theory
, hom-sets, i.e. sets of morphism
s between objects, give rise to important functor
s to the category of sets
. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
for which hom-classes are actually sets and not proper classes).
For all objects A and B in C we define two functors to the category of sets
as follows:
The functor Hom(–,B) is also called the functor of points of the object B.
Note that fixing the first argument of Hom naturally gives rise to a covariant functor and fixing the second argument naturally gives a contravariant functor. This is an artifact of the way in which one must compose the morphisms.
The pair of functors Hom(A,–) and Hom(–,B) are obviously related in a natural manner. For any pair of morphisms f : B → B′ and h : A′ → A the following diagram commutes
:

Both paths send g : A → B to f ∘ g ∘ h.
The commutativity of the above diagram implies that Hom(–,–) is a bifunctor from C × C to Set which is contravariant in the first argument and covariant in the second. Equivalently, we may say that Hom(–,–) is a covariant bifunctor
where Cop is the opposite category
to C.
gives rise to a natural transformation
and every morphism
gives rise to a natural transformation
Yoneda's lemma implies that every natural transformation between Hom functors is of this form. In other words, the Hom functors give rise to a full and faithful embedding of the category C into the functor category
SetC (covariant or contravariant depending on which Hom functor is used).
functor from A to the category Ab of abelian group
s. It is exact if and only if A is projective
.
Let R be a ring
and M a left R-module
. The functor HomZ(M,–): Ab → Mod-R is right adjoint to the tensor product
functor – R M: Mod-R → Ab.
R M: Mod-R → Ab.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, hom-sets, i.e. sets of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s between objects, give rise to important functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
Formal definition
Let C be a locally small category (i.e. a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
for which hom-classes are actually sets and not proper classes).
For all objects A and B in C we define two functors to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
as follows:
| Hom(A,–) : C → Set | Hom(–,B) : C → Set |
|---|---|
This is a covariant functor given by:
|
This is a contravariant functor given by:
Morphism In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics... s, Hom(X, B) Function (mathematics) In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
|
The functor Hom(–,B) is also called the functor of points of the object B.
Note that fixing the first argument of Hom naturally gives rise to a covariant functor and fixing the second argument naturally gives a contravariant functor. This is an artifact of the way in which one must compose the morphisms.
The pair of functors Hom(A,–) and Hom(–,B) are obviously related in a natural manner. For any pair of morphisms f : B → B′ and h : A′ → A the following diagram commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

Both paths send g : A → B to f ∘ g ∘ h.
The commutativity of the above diagram implies that Hom(–,–) is a bifunctor from C × C to Set which is contravariant in the first argument and covariant in the second. Equivalently, we may say that Hom(–,–) is a covariant bifunctor
- Hom(–,–) : Cop × C → Set
where Cop is the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
to C.
Yoneda's lemma
Referring to the above commutative diagram, one observes that every morphism- h : A′ → A
gives rise to a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
- Hom(h,–) : Hom(A,–) → Hom(A′,–)
and every morphism
- f : B → B′
gives rise to a natural transformation
- Hom(–,f) : Hom(–,B) → Hom(–,B′)
Yoneda's lemma implies that every natural transformation between Hom functors is of this form. In other words, the Hom functors give rise to a full and faithful embedding of the category C into the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
SetC (covariant or contravariant depending on which Hom functor is used).
Other properties
If A is an abelian category and A is an object of A, then HomA(A,–) is a covariant left-exactExact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
functor from A to the category Ab of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s. It is exact if and only if A is projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
.
Let R be a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and M a left R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. The functor HomZ(M,–): Ab → Mod-R is right adjoint to the tensor product
Tensor product of modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
functor –
 R M: Mod-R → Ab.
R M: Mod-R → Ab.See also
- Representable functorRepresentable functorIn mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
- Ext functorExt functorIn mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
- CurryingCurryingIn mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
- Cartesian closed categoryCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...


 for each g in Hom(A, X).
for each g in Hom(A, X). for each g in Hom(Y, B).
for each g in Hom(Y, B).