
Hilbert's syzygy theorem
Encyclopedia
In mathematics
, Hilbert's syzygy theorem is a result of commutative algebra
, first proved by David Hilbert
(1890) in connection with the syzygy
(relation) problem of invariant theory
. Roughly speaking, starting with relations between polynomial invariants, then relations between the relations, and so on, it explains how far one has to go to reach a clarified situation. It is now considered to be an early result of homological algebra
, and through the depth concept, to be a measure of the non-singularity of affine space
.
and M a finitely generated module
over the polynomial ring
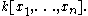
Hilbert's syzygy theorem then states that there exists a free resolution of M of length at most n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hilbert's syzygy theorem is a result of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, first proved by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
(1890) in connection with the syzygy
Syzygy (mathematics)
In mathematics, a syzygy is a relation between the generators of a module M. The set of all such relations is called the "first syzygy module of M". A relation between generators of the first syzygy module is called a "second syzygy" of M, and the set of all such relations is called the...
(relation) problem of invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
. Roughly speaking, starting with relations between polynomial invariants, then relations between the relations, and so on, it explains how far one has to go to reach a clarified situation. It is now considered to be an early result of homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, and through the depth concept, to be a measure of the non-singularity of affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
.
Formal statement
A contemporary formal statement is the following. Let k be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and M a finitely generated module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
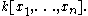
Hilbert's syzygy theorem then states that there exists a free resolution of M of length at most n.

