
Hilbert's paradox of the Grand Hotel
Encyclopedia
Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox (a non-contradictory speculation that is strongly counter-intuitive) about infinite sets presented by German mathematician David Hilbert
(1862–1943).
many rooms, all of which are occupied – that is to say every room contains a guest. One might be tempted to think that the hotel would not be able to accommodate any newly arriving guests, as would be the case with a finite number of rooms.
-loads of countably infinite passengers each. The possibility of doing so depends on the seats in the coaches being already numbered (alternatively, the hotel manager must have the axiom of countable choice
at his or her disposal). First empty the odd numbered rooms as above, then put the first coach's load in rooms 3n for n = 1, 2, 3, ..., the second coach's load in rooms 5n for n = 1, 2, ... and so on; for coach number i we use the rooms pn where p is the (i + 1)-st prime number
. You can also solve the problem by looking at the license plate numbers on the coaches and the seat numbers for the passengers (if the seats are not numbered, number them). Regard the hotel as coach #0, and the initial room numbers as the seat numbers on this coach. Interleave the digits of the coach numbers and the seat numbers to get the room numbers for the guests. The hotel (coach #0) guest in seat (original room) number 1729 moves to room 01070209 (i.e., room 1,070,209.) The passenger on seat 4935 of coach 198 goes to room 4199385 of the hotel. In general any pairing function
can be used to solve this problem. Another way to approach this is to assign everyone a number, , and which coach they are in,
, and which coach they are in,  . Those already in the hotel will be moved to room
. Those already in the hotel will be moved to room  , or the
, or the  th triangular number. Those in a coach will be in room
th triangular number. Those in a coach will be in room  , or the
, or the 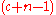 th triangular number, plus
th triangular number, plus  . In this way all the rooms will be filled by one, and only one, guest.
. In this way all the rooms will be filled by one, and only one, guest.
Some find this state of affairs profoundly counterintuitive. The properties of infinite "collections of things" are quite different from those of finite "collections of things". In an ordinary (finite) hotel with more than one room, the number of odd-numbered rooms is obviously smaller than the total number of rooms. However, in Hilbert's aptly named Grand Hotel, the quantity of odd-numbered rooms is as many as the total quantity of rooms. In mathematical terms, the cardinality of the subset
containing the odd-numbered rooms is the same as the cardinality of the set of all rooms. Indeed, infinite sets are characterized as sets that have proper subsets of the same cardinality. For countable sets, this cardinality is called (aleph-null
(aleph-null
).
Rephrased, for any countably infinite set, there exists a bijective function which maps the countably infinite set to the set of natural numbers, even if the countably infinite set contains the natural numbers. For example, the set of rational numbers - those numbers which can be written as a quotient of integers - contains the natural numbers as a subset, but is no bigger than the set of natural numbers since the rationals are countable: There is a bijection from the naturals to the rationals.
only works from an induction basis.
Suppose that the Grand Hotel does not allow smoking, and no cigars may be taken into the Hotel. Despite this, the guest in room 1 goes to the guest in room 2 to get a cigar. The guest in room 2 goes to room 3 to get two cigars - one for himself and one for the guest in room 1. In general, the guest in room N goes to room (N+1) to get N cigars. They each return, smoke one cigar and give the rest to the guest from room (N-1). Thus despite the fact no cigars have been brought into the hotel, each guest can smoke a cigar inside the property.
The fallacy of this story derives from the fact that there is no inductive point (base-case) from which the induction can derive. Although it is shown that if the guest from room N has N cigars then both he and all guests in lower-numbered rooms can smoke, it is never proved that any of the guests actually have cigars therefore it doesn't follow that any guest can smoke a cigar inside the Hotel. The fact that the story mentions that cigars are not allowed into the hotel is designed to highlight the fallacy.
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
(1862–1943).
The paradox
Consider a hypothetical hotel with countably infinitelyCountable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
many rooms, all of which are occupied – that is to say every room contains a guest. One might be tempted to think that the hotel would not be able to accommodate any newly arriving guests, as would be the case with a finite number of rooms.
Finitely many new guests
Suppose a new guest arrives and wishes to be accommodated in the hotel. Because the hotel has infinitely many rooms, we can move the guest occupying room 1 to room 2, the guest occupying room 2 to room 3 and so on, and fit the newcomer into room 1. By repeating this procedure, it is possible to make room for any finite number of new guests.Infinitely many new guests
It is also possible to accommodate a countably infinite number of new guests: just move the person occupying room 1 to room 2, the guest occupying room 2 to room 4, and in general room n to room 2n, and all the odd-numbered rooms will be free for the new guests.Infinitely many coaches with infinitely many guests each
It is possible to accommodate countably infinitely many coachCoach (vehicle)
A coach is a large motor vehicle, a type of bus, used for conveying passengers on excursions and on longer distance express coach scheduled transport between cities - or even between countries...
-loads of countably infinite passengers each. The possibility of doing so depends on the seats in the coaches being already numbered (alternatively, the hotel manager must have the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
at his or her disposal). First empty the odd numbered rooms as above, then put the first coach's load in rooms 3n for n = 1, 2, 3, ..., the second coach's load in rooms 5n for n = 1, 2, ... and so on; for coach number i we use the rooms pn where p is the (i + 1)-st prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. You can also solve the problem by looking at the license plate numbers on the coaches and the seat numbers for the passengers (if the seats are not numbered, number them). Regard the hotel as coach #0, and the initial room numbers as the seat numbers on this coach. Interleave the digits of the coach numbers and the seat numbers to get the room numbers for the guests. The hotel (coach #0) guest in seat (original room) number 1729 moves to room 01070209 (i.e., room 1,070,209.) The passenger on seat 4935 of coach 198 goes to room 4199385 of the hotel. In general any pairing function
Pairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
can be used to solve this problem. Another way to approach this is to assign everyone a number,
 , and which coach they are in,
, and which coach they are in,  . Those already in the hotel will be moved to room
. Those already in the hotel will be moved to room  , or the
, or the  th triangular number. Those in a coach will be in room
th triangular number. Those in a coach will be in room  , or the
, or the 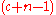 th triangular number, plus
th triangular number, plus  . In this way all the rooms will be filled by one, and only one, guest.
. In this way all the rooms will be filled by one, and only one, guest.Analysis
These cases demonstrate the 'paradox', by which we mean not that it is contradictory, but rather that a counter-intuitive result is provably true: The situations "there is a guest to every room" and "no more guests can be accommodated" are not equivalent when there are infinitely many rooms.Some find this state of affairs profoundly counterintuitive. The properties of infinite "collections of things" are quite different from those of finite "collections of things". In an ordinary (finite) hotel with more than one room, the number of odd-numbered rooms is obviously smaller than the total number of rooms. However, in Hilbert's aptly named Grand Hotel, the quantity of odd-numbered rooms is as many as the total quantity of rooms. In mathematical terms, the cardinality of the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
containing the odd-numbered rooms is the same as the cardinality of the set of all rooms. Indeed, infinite sets are characterized as sets that have proper subsets of the same cardinality. For countable sets, this cardinality is called
 (aleph-null
(aleph-nullAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
).
Rephrased, for any countably infinite set, there exists a bijective function which maps the countably infinite set to the set of natural numbers, even if the countably infinite set contains the natural numbers. For example, the set of rational numbers - those numbers which can be written as a quotient of integers - contains the natural numbers as a subset, but is no bigger than the set of natural numbers since the rationals are countable: There is a bijection from the naturals to the rationals.
The Grand Hotel Cigar Mystery
Another story regarding the Grand Hotel can be used to show that mathematical inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
only works from an induction basis.
Suppose that the Grand Hotel does not allow smoking, and no cigars may be taken into the Hotel. Despite this, the guest in room 1 goes to the guest in room 2 to get a cigar. The guest in room 2 goes to room 3 to get two cigars - one for himself and one for the guest in room 1. In general, the guest in room N goes to room (N+1) to get N cigars. They each return, smoke one cigar and give the rest to the guest from room (N-1). Thus despite the fact no cigars have been brought into the hotel, each guest can smoke a cigar inside the property.
The fallacy of this story derives from the fact that there is no inductive point (base-case) from which the induction can derive. Although it is shown that if the guest from room N has N cigars then both he and all guests in lower-numbered rooms can smoke, it is never proved that any of the guests actually have cigars therefore it doesn't follow that any guest can smoke a cigar inside the Hotel. The fact that the story mentions that cigars are not allowed into the hotel is designed to highlight the fallacy.
External links
- Hilbert infinite hotel. M. Hazewinkel. Encyclopedia of Mathematics, Springer. Accessed May 25, 2007.
- Welcome to the Hotel Infinity! — The paradox told as a humorous narrative, featuring a hotel owner and a building contractor based on the feuding 19th-century mathematicians Georg CantorGeorg CantorGeorg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
and Leopold KroneckerLeopold KroneckerLeopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"... - Steven Strogatz, The Hilbert Hotel, NY Times, May 9, 2010
- Nancy Casey, Welcome to the Hotel Infinity!
- Hilbert's Infinite Hotel, h2g2
- The Hilbert Hotel - YouTube presentation

