
Highly composite number
Encyclopedia
A highly composite number (HCN) is a positive integer
with more divisor
s than any positive integer smaller than itself.
The initial or smallest twenty-one highly composite numbers are listed in the table at right.
The sequence of highly composite numbers is a subset of the sequence of smallest numbers k with exactly n divisors .
There are an infinite number of highly composite numbers. To prove
this fact, suppose that n is an arbitrary highly composite number. Then 2n has more divisors than n (2n itself is a divisor and so are all the divisors of n) and so some number larger than n (and not larger than 2n) must be highly composite as well.
Roughly speaking, for a number to be highly composite it has to have prime
factors as small as possible, but not too many of the same. If we decompose a number n in prime factors like this:

where are prime, and the exponents
are prime, and the exponents  are positive integers, then the number of divisors of n is exactly
are positive integers, then the number of divisors of n is exactly

Hence, for n to be a highly composite number,
Also, except in two special cases n = 4 and n = 36, the last exponent ck must equal 1. Saying that the sequence of exponents is non-increasing is equivalent to saying that a highly composite number is a product of primorials. Because the prime factorization of a highly composite number uses all of the first k primes, every highly composite number must be a practical number
.
Highly composite numbers higher than 6 are also abundant numbers. One need only look at the three or four highest divisors of a particular highly composite number to ascertain this fact. It is false that all highly composite numbers are also Harshad number
s in base 10. The first HCN that is not a Harshad number is 245,044,800, which has a digit sum of 27, but 27 does not divide evenly into 245,044,800.
Many of these numbers are used in traditional systems of measurement, and tend to be used in engineering designs, due to their ease of use in calculations involving vulgar fractions.
If Q(x) denotes the number of highly composite numbers less than or equal to x, then there are two constants a and b, both greater than 1, such that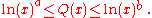
The first part of the inequality was proved by Paul Erdős in 1944 and the second part by Jean-Louis Nicolas in 1988.
The 15,000th highly composite number can be found on Achim Flammenkamp's website. It is the product of 230 primes:
where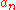 is the sequence of successive prime numbers, and all omitted terms (a22 to a228) are factors with exponent equal to one (i.e. the number is
is the sequence of successive prime numbers, and all omitted terms (a22 to a228) are factors with exponent equal to one (i.e. the number is  ).
).
If this were untrue for any particular highly composite number and subset of prime factors, we could exchange that subset of primefactors and exponents for the smaller number using the same primefactors and get a smaller number with at least as many divisors.
This property is useful for finding highly composite numbers.
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
with more divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s than any positive integer smaller than itself.
The initial or smallest twenty-one highly composite numbers are listed in the table at right.
 |
number of divisors of  |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 4 | 3 |
| 6 | 4 |
| 12 12 (number) 12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten... |
6 |
| 24 24 (number) 24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto... |
8 |
| 36 36 (number) 36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number... |
9 |
| 48 48 (number) 48 is the natural number following 47 and preceding 49. It is one third of a gross or four dozens.- In mathematics :Forty-eight is a double factorial of 6, a highly composite number. Like all other multiples of 6, it is a semiperfect number. 48 is the second 17-gonal number.48 is in abundance... |
10 |
| 60 60 (number) 60 is the natural number following 59 and preceding 61. Being three times twenty, 60 is called "three score" in some older literature.-In mathematics:... |
12 |
| 120 120 (number) 120 is the natural number following 119 and preceding 121. 120 was known as "the great hundred", especially prior to the year 1700, from the Teutonic Hundert which equalled 120. The number 100, now known commonly as "one hundred" was then known as "the small hundred". It is also known as... |
16 |
| 180 180 (number) 180 is the natural number following 179 and preceding 181.-In mathematics:180 is an abundant number, with its proper divisors summing up to 366. 180 is also a highly composite number, a positive integer with more divisors than any smaller positive integer... |
18 |
| 240 240 (number) 240 is the natural number following 239 and preceding 241.-In mathematics:With 20 divisors total , more than any previous number, 240 is a highly composite number, and it is also a refactorable number or tau number, since it has 20 divisors and 20 divides 240... |
20 |
| 360 360 (number) 360 or three sixty is the natural number following 359 and preceding 361.-In mathematics:*Divisors are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 and 360. *360 makes a highly composite number... |
24 |
| 720 720 (number) Seven hundred twenty is the natural number following 719 and preceding 721.It is 6! , a composite number with thirty divisors, more than any number below, making it a highly composite number... |
30 |
| 840 | 32 |
| 1,260 | 36 |
| 1,680 | 40 |
| 2,520 | 48 |
| 5,040 5040 (number) 5040 is a factorial , a highly composite number, a superior highly composite number, a colossally abundant number, and the number of permutations of 4 items out of 10 choices .-Philosophy:... |
60 |
| 7,560 | 64 |
| 10,080 | 72 |
The sequence of highly composite numbers is a subset of the sequence of smallest numbers k with exactly n divisors .
There are an infinite number of highly composite numbers. To prove
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
this fact, suppose that n is an arbitrary highly composite number. Then 2n has more divisors than n (2n itself is a divisor and so are all the divisors of n) and so some number larger than n (and not larger than 2n) must be highly composite as well.
Roughly speaking, for a number to be highly composite it has to have prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
factors as small as possible, but not too many of the same. If we decompose a number n in prime factors like this:

where
 are prime, and the exponents
are prime, and the exponents  are positive integers, then the number of divisors of n is exactly
are positive integers, then the number of divisors of n is exactly
Hence, for n to be a highly composite number,
- the k given prime numbers pi must be precisely the first k prime numbers (2, 3, 5, ...); if not, we could replace one of the given primes by a smaller prime, and thus obtain a smaller number than n with the same number of divisors (for instance 10 = 2 × 5 may be replaced with 6 = 2 × 3; both have 4 divisors);
- the sequence of exponents must be non-increasing, that is
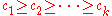 ; otherwise, by exchanging two exponents we would again get a smaller number than n with the same number of divisors (for instance 18 = 21 × 32 may be replaced with 12 = 22 × 31; both have six divisors).
; otherwise, by exchanging two exponents we would again get a smaller number than n with the same number of divisors (for instance 18 = 21 × 32 may be replaced with 12 = 22 × 31; both have six divisors).
Also, except in two special cases n = 4 and n = 36, the last exponent ck must equal 1. Saying that the sequence of exponents is non-increasing is equivalent to saying that a highly composite number is a product of primorials. Because the prime factorization of a highly composite number uses all of the first k primes, every highly composite number must be a practical number
Practical number
In number theory, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisors of n...
.
Highly composite numbers higher than 6 are also abundant numbers. One need only look at the three or four highest divisors of a particular highly composite number to ascertain this fact. It is false that all highly composite numbers are also Harshad number
Harshad number
A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
s in base 10. The first HCN that is not a Harshad number is 245,044,800, which has a digit sum of 27, but 27 does not divide evenly into 245,044,800.
Many of these numbers are used in traditional systems of measurement, and tend to be used in engineering designs, due to their ease of use in calculations involving vulgar fractions.
If Q(x) denotes the number of highly composite numbers less than or equal to x, then there are two constants a and b, both greater than 1, such that
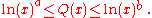
The first part of the inequality was proved by Paul Erdős in 1944 and the second part by Jean-Louis Nicolas in 1988.
Examples
| The highly composite number : 10,080. 10,080 = (2 × 2 × 2 × 2 × 2) × (3 × 3) × 5 × 7 By (2) above, 10,080 has exactly seventy-two divisors. |
|||||
| 1 × 10,080 |
2 × 5,040 |
3 × 3,360 |
4 × 2,520 |
5 × 2,016 |
6 × 1,680 |
| 7 × 1,440 |
8 × 1,260 |
9 × 1,120 |
10 × 1,008 |
12 × 840 |
14 × 720 |
| 15 × 672 |
16 × 630 |
18 × 560 |
20 × 504 |
21 × 480 |
24 × 420 |
| 28 × 360 |
30 × 336 |
32 × 315 |
35 × 288 |
36 × 280 |
40 × 252 |
| 42 × 240 |
45 × 224 |
48 × 210 |
56 × 180 |
60 × 168 |
63 × 160 |
| 70 × 144 |
72 × 140 |
80 × 126 |
84 × 120 |
90 × 112 |
96 × 105 |
| Note: The bolded numbers are themselves highly composite numbers. Only the twentieth highly composite number 7560 (=3×2520) is absent. |
| 10080 is a so-called 7-smooth number Smooth number In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:... , . |
The 15,000th highly composite number can be found on Achim Flammenkamp's website. It is the product of 230 primes:
-
 ,
,
where
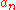 is the sequence of successive prime numbers, and all omitted terms (a22 to a228) are factors with exponent equal to one (i.e. the number is
is the sequence of successive prime numbers, and all omitted terms (a22 to a228) are factors with exponent equal to one (i.e. the number is  ).
). Prime factor subsets
For any highly composite number, if one takes any subset of prime factors for that number and their exponents, the resulting number will have more divisors than any smaller number that uses the same prime factors. For example for the highly composite number 720 which is 24 × 32 × 5 we can be sure that- 144 which is 24 × 32 has more divisors than any smaller number that has only the prime factors 2 and 3
- 80 which is 24 × 5 has more divisors than any smaller number that has only the prime factors 2 and 5
- 45 which is 32 × 5 has more divisors than any smaller number that has only the prime factors 3 and 5
If this were untrue for any particular highly composite number and subset of prime factors, we could exchange that subset of primefactors and exponents for the smaller number using the same primefactors and get a smaller number with at least as many divisors.
This property is useful for finding highly composite numbers.

