Harmonic map
Encyclopedia
A map φ:M→N between Riemannian manifolds M and N is called harmonic if it is a critical point
of the Dirichlet energy
functional
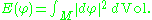
This functional E will be defined precisely below—one way of understanding it is to imagine that M is made of rubber
and N made of marble
(their shapes given by their respective metrics
), and that the map φ:M→N prescribes how one "applies" the rubber onto the marble: E(φ) then represents the total amount of elastic potential energy resulting from tension in the rubber. In these terms, φ is a harmonic map if the rubber, when "released" but still constrained to stay everywhere in contact with the marble, already finds itself in a position of equilibrium and therefore does not "snap" into a different shape.
Harmonic maps are the 'least expanding' maps in orthogonal directions.
Existence of harmonic maps from a complete Riemannian manifold to a complete Riemannian manifold of non-positive sectional curvature was proved by .
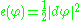
where the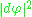
is the squared norm of the differential of φ, with respect to the induced metric on the bundle T*M⊗φ−1TN. The total energy of φ is given by integrating the density over M
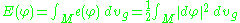
where dvg denotes the measure
on M induced by its metric. This generalizes the classical Dirichlet energy
.
The energy density can be written more explicitly as
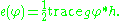
Using the Einstein summation convention, in local coordinates
the right hand side of this equality reads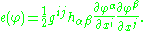
If M is compact, then φ is called a harmonic map if it is a critical point of the energy functional E. This definition is extended to the case where M is not compact by requiring the restriction of φ to every compact domain to be harmonic, or, more typically, requiring that φ be a critical point of the energy functional in the Sobolev space
H1,2(M,N).
Equivalently, the map φ is harmonic if it satisfies the Euler-Lagrange equations
associated to the functional E. These equations read
where ∇ is the connection on the vector bundle
T*M⊗φ−1(TN) induced by the Levi-Civita connection
s on M and N. The quantity τ(φ) is a section of the bundle φ−1(TN) known as the tension
field of φ. In terms of the physical analogy, it corresponds to the direction in which the "rubber" manifold M will tend to move in N in seeking the energy-minimizing configuration.
s . The energy integrand is instead a function of the form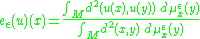
in which μ is a family of measures
attached to each point of M.
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
of the Dirichlet energy
Dirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
functional
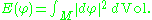
This functional E will be defined precisely below—one way of understanding it is to imagine that M is made of rubber
Rubber
Natural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...
and N made of marble
Marble
Marble is a metamorphic rock composed of recrystallized carbonate minerals, most commonly calcite or dolomite.Geologists use the term "marble" to refer to metamorphosed limestone; however stonemasons use the term more broadly to encompass unmetamorphosed limestone.Marble is commonly used for...
(their shapes given by their respective metrics
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
), and that the map φ:M→N prescribes how one "applies" the rubber onto the marble: E(φ) then represents the total amount of elastic potential energy resulting from tension in the rubber. In these terms, φ is a harmonic map if the rubber, when "released" but still constrained to stay everywhere in contact with the marble, already finds itself in a position of equilibrium and therefore does not "snap" into a different shape.
Harmonic maps are the 'least expanding' maps in orthogonal directions.
Existence of harmonic maps from a complete Riemannian manifold to a complete Riemannian manifold of non-positive sectional curvature was proved by .
Mathematical definition
Given Riemannian manifolds (M,g), (N,h) and φ as above, the energy density of φ at a point x in M is defined as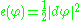where the
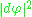is the squared norm of the differential of φ, with respect to the induced metric on the bundle T*M⊗φ−1TN. The total energy of φ is given by integrating the density over M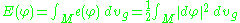where dvg denotes the measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on M induced by its metric. This generalizes the classical Dirichlet energy
Dirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
.
The energy density can be written more explicitly as
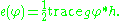
Using the Einstein summation convention, in local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
the right hand side of this equality reads
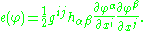
If M is compact, then φ is called a harmonic map if it is a critical point of the energy functional E. This definition is extended to the case where M is not compact by requiring the restriction of φ to every compact domain to be harmonic, or, more typically, requiring that φ be a critical point of the energy functional in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
H1,2(M,N).
Equivalently, the map φ is harmonic if it satisfies the Euler-Lagrange equations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
associated to the functional E. These equations read
where ∇ is the connection on the vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
T*M⊗φ−1(TN) induced by the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
s on M and N. The quantity τ(φ) is a section of the bundle φ−1(TN) known as the tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
field of φ. In terms of the physical analogy, it corresponds to the direction in which the "rubber" manifold M will tend to move in N in seeking the energy-minimizing configuration.
Examples
- Identity and constant maps are harmonic.
- Assume that the source manifold M is the real line R (or the circle S1), i.e. that φ is a curve (or a closed curve) on N. Then φ is a harmonic map if and only if it is a geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
. (In this case, the rubber-and-marble analogy described above reduces to the usual elastic band analogy for geodesics.) - Assume that the target manifold N is Euclidean space Rn (with its standard metric). Then φ is a harmonic map if and only if it is a harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
in the usual sense (i.e. a solution of the Laplace equation). This follows from the Dirichlet principle. If φ is a diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
onto an open set in Rn, then it gives a harmonic coordinate systemHarmonic coordinatesIn Riemannian geometry, a branch of mathematics, harmonic coordinates are a coordinate system on a Riemannian manifold each of whose coordinate functions xi is harmonic, meaning that it satisfies Laplace's equation\Delta x^i = 0.\,...
. - Every minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
in Euclidean space is a harmonic immersion. - More generally, a minimal submanifold M of N is a harmonic immersion of N in M.
- Every totally geodesic map is harmonic (in this case, ∇dφ*h itself vanishes, not just its trace).
- Every holomorphic map between Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s is harmonic.
Problems and applications
- If, after applying the rubber M onto the marble N via some map φ, one "releases" it, it will try to "snap" into a position of least tension. This "physical" observation leads to the following mathematical problem: given a homotopy class of maps from M to N, does it contain a representative that is a harmonic map?
- Existence results on harmonic maps between manifolds has consequences for their curvatureRiemann curvature tensorIn the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. - Once existence is known, how can a harmonic map be constructed explicitly? (One fruitful method uses twistor theoryTwistor theoryIn theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
.) - In theoretical physicsTheoretical physicsTheoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, harmonic maps are also known as sigma models. - One of the original ideas in grid generation methods for computational fluid dynamics and computational physics was to use either conformal or harmonic mapping to generate regular grids.
Harmonic maps between metric spaces
The energy integral can be formulated in a weaker setting for functions between two metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s . The energy integrand is instead a function of the form
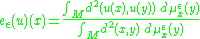
in which μ is a family of measures
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
attached to each point of M.