Group Hopf algebra
Encyclopedia
In mathematics, the group Hopf algebra of a given group
is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.
and k a field
. The group Hopf algebra of G over k, denoted kG (or k[G]), is as a set (and vector space) the free vector space on G over k. As an algebra
, its product is defined by linear extension of the group composition in G, with multiplicative unit the identity in G; this product is also known as convolution
.
Note that while the group algebra of a finite group can be identified with the space of functions on the group, for an infinite group these are different. The group algebra, consisting of finite sums, corresponds to functions on the group that vanish for cofinitely many points; topologically (using the discrete topology), these correspond to functions with compact support.
However, the group algebra k[G] and the space of function kG := Hom(G,k) are dual: given an element of the group algebra
and a function on the group 
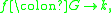these pair to give an element of k via 
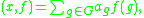which is a well-defined sum because it is finite.
by defining the coproduct, counit, and antipode to be the linear extensions of the following maps defined on G:
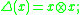
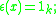
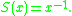
The required Hopf algebra compatibility axioms are easily checked. Notice that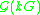
, the set of group-like elements of kG (i.e. elements 
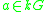such that 
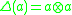and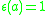 
), is precisely G.
. Any action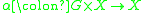
of G on X gives a homomorphism 
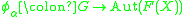, where F(X) is an appropriate algebra of k-valued functions, such as the Gelfand-Naimark algebra 
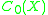of continuous function
s vanishing at infinity.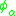
is defined by 
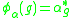with the adjoint 
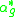defined by
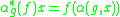
for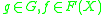
, and 
.
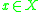This may be described by a linear mapping
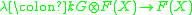
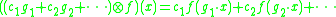
where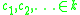
, 
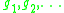are the elements of G, and 
, which has the property that group-like elements in kG give rise to automorphisms of F(X).
endows F(X) with an important extra structure, described below.
over the algebra H such that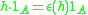
and
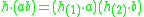
whenever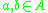
, 
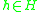and 
in sumless Sweedler notation. Obviously,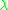 
as defined in the previous section turns 
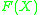into a left Hopf kG-module algebra, and hence allows us to consider the following construction.
Let H be a Hopf algebra and A a left Hopf H-module algebra. The smash product algebra
is the vector space 
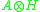with the product
,
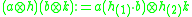and we write
for 
in this context.
In our case, A = F(X) and H = kG, and we have
.
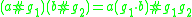In this case the smash product algebra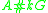
is also denoted by 
.
The cyclic homology of Hopf smash products has been computed. However, there the smash product is called a crossed product and denoted
- not to be confused with the crossed product derived from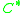 
-dynamical systems.
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.
Definition
Let G be an arbitrary groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and k a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. The group Hopf algebra of G over k, denoted kG (or k[G]), is as a set (and vector space) the free vector space on G over k. As an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, its product is defined by linear extension of the group composition in G, with multiplicative unit the identity in G; this product is also known as convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
.
Note that while the group algebra of a finite group can be identified with the space of functions on the group, for an infinite group these are different. The group algebra, consisting of finite sums, corresponds to functions on the group that vanish for cofinitely many points; topologically (using the discrete topology), these correspond to functions with compact support.
However, the group algebra k[G] and the space of function kG := Hom(G,k) are dual: given an element of the group algebra
and a function on the group 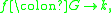these pair to give an element of k via 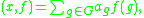which is a well-defined sum because it is finite.Hopf algebra structure
We give kG the structure of a cocommutative Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
by defining the coproduct, counit, and antipode to be the linear extensions of the following maps defined on G:
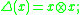
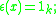
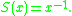
The required Hopf algebra compatibility axioms are easily checked. Notice that
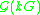, the set of group-like elements of kG (i.e. elements 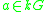such that 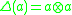and 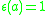), is precisely G.Symmetries of group actions
Let G be a group and X a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Any action
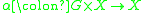of G on X gives a homomorphism 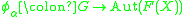, where F(X) is an appropriate algebra of k-valued functions, such as the Gelfand-Naimark algebra of continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s vanishing at infinity.
is defined by with the adjoint 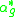defined by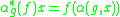for
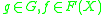, and 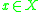.This may be described by a linear mapping
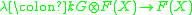
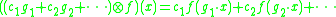
where
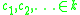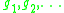, are the elements of G, and , which has the property that group-like elements in kG give rise to automorphisms of F(X).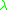 endows F(X) with an important extra structure, described below.Hopf module algebras and the Hopf smash product
Let H be a Hopf algebra. A (left) Hopf H-module algebra A is an algebra which is a (left) moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the algebra H such that
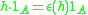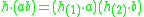
andwhenever
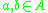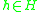, and in sumless Sweedler notation. Obviously, 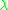as defined in the previous section turns 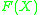into a left Hopf kG-module algebra, and hence allows us to consider the following construction.Let H be a Hopf algebra and A a left Hopf H-module algebra. The smash product algebra
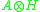is the vector space with the product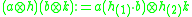,and we write
for in this context.In our case, A = F(X) and H = kG, and we have
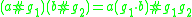.In this case the smash product algebra
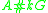is also denoted by .The cyclic homology of Hopf smash products has been computed. However, there the smash product is called a crossed product and denoted
- not to be confused with the crossed product derived from -dynamical systems.