Green's relations
Encyclopedia
In mathematics
, Green's relations are five equivalence relation
s that characterise the elements of a semigroup
in terms of the principal ideal
s they generate. The relations are named for James Alexander Green
, who introduced them in a paper of 1951. John Mackintosh Howie
, a prominent semigroup theorist, described this work as "so all-pervading that, on encountering a new semigroup, almost the first question one asks is 'What are the Green relations like?'" (Howie 2002). The relations are useful for understanding the nature of divisibility in a semigroup; they are also valid for groups
, but in this case tell us nothing useful, because groups always have divisibility. (In the same way, the ideals of a field
are a much less rich environment for study than the ideals of a ring
.)
Instead of working directly with a semigroup S, we define Green's relations over the monoid
S1. (S1 is "S with an identity adjoined if necessary"; if S is not already a monoid, a new element is adjoined and defined to be an identity.) This ensures that principal ideals generated by some semigroup element do indeed contain that element. For an element a of S, the relevant ideals are:
That is, a and b are L-related if they generate the same left ideal; R-related if they generate the same right ideal; and J-related if they generate the same two-sided ideal. These are equivalence relations on S, so each of them yields a partition of S into equivalence classes. The L-class of a is denoted La (and similarly for the other relations).
Green used the lowercase blackletter
, 
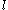and 
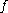for these relations, and wrote 
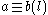for a L b (and likewise for R and J). Mathematicians today tend to use script letters such as 
instead, and replace Green's modular arithmetic
-style notation with the infix style used here. Ordinary letters are used for the equivalence classes.
The L and R relations are left-right dual to one another; theorems concerning one can be translated into similar statements about the other. For example, L is right-compatible: if a L b and c is another element of S, then ac L bc. Dually, R is left-compatible: if a R b, then ca R cb.
If S is commutative, then L, R and J coincide.
This is also an equivalence relation on S. The class Ha is the intersection of La and Ra. More generally, the intersection of any L-class with any R-class is either an H-class or the empty set.
Green's Theorem states that for any H-class H of a subgroup S either (i)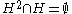
or (ii) 
and H is a subgroup of S. An important corollary is that the equivalence class He, where e is an idempotent, is a subgroup of S (its identity is e, and all elements have inverses), and indeed is the largest subgroup of S containing e. No H-class can contain more than one idempotent, thus H is idempotent separating. In a monoid M, H1 is traditionally called the group of units. (Beware that unit does not mean identity in this context, i.e. in general there are non-identity elements in H1. The "unit" terminology comes from ring theory
.) For example, in the transformation monoid on n elements, Tn, the group of units is the symmetric group
Sn.
Finally, D is defined by : a D b if and only if there exists a c in S such that a L c and c R b. In the language of lattices
, D is the join of L and R. (The join for equivalence relations is normally more difficult to define, but is simplified in this case by the fact that a L c and c R b for some c if and only if a R d and d L b for some d.)
As D is the smallest equivalence relation containing both L and R, we know that a D b implies a J b — so J contains D. In a finite semigroup, D and J are the same.
There is also a formulation of D in terms of equivalence classes, derived directly from the above definition:
Consequently, the D-classes of a semigroup can be seen as unions of L-classes, as unions of R-classes, or as unions of H-classes. Clifford and Preston (1961) suggest thinking of this situation in terms of an egg-box:
Each row of eggs represents an R-class, and each column an L-class; the eggs themselves are the H-classes. For a group, there is only one egg, because all five of Green's relations coincide, and make all group elements equivalent. The opposite case, found for example in the bicyclic semigroup
, is where each element is in an H-class of its own. The egg-box for this semigroup would contain infinitely many eggs, but all eggs are in the same box because there is only one D-class. (A semigroup for which all elements are D-related is called bisimple.)
It can be shown that within a D-class, all H-classes are the same size. For example, the transformation semigroup T4 contains four D-classes, within which the H-classes have 1, 2, 6, and 24 elements respectively.
Recent advances in the combinatorics
of semigroups have used Green's relations to help enumerate semigroups with certain properties. A typical result (Satoh, Yama, and Tokizawa 1994) shows that there are exactly 1,843,120,128 non-equivalent semigroups of order 8, including 221,805 which are commutative; their work is based on a systematic exploration of possible D-classes. (By contrast, there are only five groups of order 8.)
The egg-box diagram for T3 has three D-classes. They are also J-classes, because these relations coincide for a finite semigroup.
In T3, two functions are L-related if and only if they have the same image
. Such functions appear in the same column of the table above. Likewise, the functions f and g are R-related if and only if
for x and y in {1, 2, 3}; such functions are in the same table row. Consequently, two functions are D-related if and only if their images are the same size.
The elements in bold are the idempotents. Any H-class containing one of these is a (maximal) subgroup. In particular, the third D-class is isomorphic to the symmetric group S3. There are also six subgroups of order 2, and three of order 1 (as well as subgroups of these subgroups). Six elements of T3 are not in any subgroup.
Following the first route, analogous versions of Green's relations have been defined for semiring
s (Grillet 1970) and rings (Petro 2002). Some, but not all, of the properties associated with the relations in semigroups carry over to these cases. Staying within the world of semigroups, Green's relations can be extended to cover relative ideals, which are subsets that are only ideals with respect to a subsemigroup (Wallace 1963).
For the second kind of generalisation, researchers have concentrated on properties of bijection
s between L- and R- classes. If x R y, then it is always possible to find bijections between Lx and Ly that are R-class-preserving. (That is, if two elements of an L-class are in the same R-class, then their images under a bijection will still be in the same R-class.) The dual statement for x L y also holds. These bijections are right and left translations, restricted to the appropriate equivalence classes. The question that arises is: how else could there be such bijections?
Suppose that Λ and Ρ are semigroups of partial transformations of some semigroup S. Under certain conditions, it can be shown that if x Ρ = y Ρ, with x ρ1 = y and y ρ2 = x, then the restrictions
are mutually inverse bijections. (Conventionally, arguments are written on the right for Λ, and on the left for Ρ.) Then the L and R relations can be defined by
and D and H follow as usual. Generalisation of J is not part of this system, as it plays no part in the desired property.
We call (Λ, Ρ) a Green's pair. There are several choices of partial transformation semigroup that yield the original relations. One example would be to take Λ to be the semigroup of all left translations on S1, restricted to S, and Ρ the corresponding semigroup of restricted right translations.
These definitions are due to Clark and Carruth (1980). They subsume Wallace's work, as well as various other generalised definitions proposed in the mid-1970s. The full axioms are fairly lengthy to state; informally, the most important requirements are that both Λ and Ρ should contain the identity transformation, and that elements of Λ should commute with elements of Ρ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Green's relations are five equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s that characterise the elements of a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
in terms of the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
s they generate. The relations are named for James Alexander Green
James Alexander Green
James Alexander "Sandy" Green FRS is a mathematician and retired Professor at the Mathematics Institute at the University of Warwick, who is still active in the field of representation theory.-Early life:...
, who introduced them in a paper of 1951. John Mackintosh Howie
John Mackintosh Howie
John Mackintosh Howie, CBE, FRSE , Scottish mathematician, is a prominent semigroup theorist.Howie was educated at Robert Gordon's College, Aberdeen, the University of Aberdeenand Balliol College, Oxford....
, a prominent semigroup theorist, described this work as "so all-pervading that, on encountering a new semigroup, almost the first question one asks is 'What are the Green relations like?'" (Howie 2002). The relations are useful for understanding the nature of divisibility in a semigroup; they are also valid for groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, but in this case tell us nothing useful, because groups always have divisibility. (In the same way, the ideals of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
are a much less rich environment for study than the ideals of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.)
Instead of working directly with a semigroup S, we define Green's relations over the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
S1. (S1 is "S with an identity adjoined if necessary"; if S is not already a monoid, a new element is adjoined and defined to be an identity.) This ensures that principal ideals generated by some semigroup element do indeed contain that element. For an element a of S, the relevant ideals are:
- The principal left ideal generated by a:
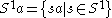. This is the same as 
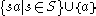, which is 
. - The principal right ideal generated by a:
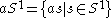, or equivalently 
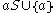. - The principal two-sided ideal generated by a:
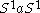, or 
.
The L, R, and J relations
For elements a and b of S, Green's relations L, R and J are defined by- a L b if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
S1 a = S1 b. - a R b if and only if a S1 = b S1.
- a J b if and only if S1 a S1 = S1 b S1.
That is, a and b are L-related if they generate the same left ideal; R-related if they generate the same right ideal; and J-related if they generate the same two-sided ideal. These are equivalence relations on S, so each of them yields a partition of S into equivalence classes. The L-class of a is denoted La (and similarly for the other relations).
Green used the lowercase blackletter
Blackletter
Blackletter, also known as Gothic script, Gothic minuscule, or Textura, was a script used throughout Western Europe from approximately 1150 to well into the 17th century. It continued to be used for the German language until the 20th century. Fraktur is a notable script of this type, and sometimes...
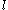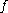, and for these relations, and wrote 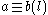for a L b (and likewise for R and J). Mathematicians today tend to use script letters such as instead, and replace Green's modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
-style notation with the infix style used here. Ordinary letters are used for the equivalence classes.
The L and R relations are left-right dual to one another; theorems concerning one can be translated into similar statements about the other. For example, L is right-compatible: if a L b and c is another element of S, then ac L bc. Dually, R is left-compatible: if a R b, then ca R cb.
If S is commutative, then L, R and J coincide.
The H and D relations
The remaining relations are derived from L and R. Their intersection is H:- a H b if and only if a L b and a R b.
This is also an equivalence relation on S. The class Ha is the intersection of La and Ra. More generally, the intersection of any L-class with any R-class is either an H-class or the empty set.
Green's Theorem states that for any H-class H of a subgroup S either (i)
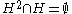or (ii) and H is a subgroup of S. An important corollary is that the equivalence class He, where e is an idempotent, is a subgroup of S (its identity is e, and all elements have inverses), and indeed is the largest subgroup of S containing e. No H-class can contain more than one idempotent, thus H is idempotent separating. In a monoid M, H1 is traditionally called the group of units. (Beware that unit does not mean identity in this context, i.e. in general there are non-identity elements in H1. The "unit" terminology comes from ring theoryUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
.) For example, in the transformation monoid on n elements, Tn, the group of units is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn.
Finally, D is defined by : a D b if and only if there exists a c in S such that a L c and c R b. In the language of lattices
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, D is the join of L and R. (The join for equivalence relations is normally more difficult to define, but is simplified in this case by the fact that a L c and c R b for some c if and only if a R d and d L b for some d.)
As D is the smallest equivalence relation containing both L and R, we know that a D b implies a J b — so J contains D. In a finite semigroup, D and J are the same.
There is also a formulation of D in terms of equivalence classes, derived directly from the above definition:
- a D b if and only if the intersection of Ra and Lb is not empty.
Consequently, the D-classes of a semigroup can be seen as unions of L-classes, as unions of R-classes, or as unions of H-classes. Clifford and Preston (1961) suggest thinking of this situation in terms of an egg-box:
Each row of eggs represents an R-class, and each column an L-class; the eggs themselves are the H-classes. For a group, there is only one egg, because all five of Green's relations coincide, and make all group elements equivalent. The opposite case, found for example in the bicyclic semigroup
Bicyclic semigroup
In mathematics, the bicyclic semigroup is an algebraic object important for the structure theory of semigroups. Although it is in fact a monoid, it is usually referred to as simply a semigroup. The first published description of this object was given by Evgenii Lyapin in 1953. Alfred H...
, is where each element is in an H-class of its own. The egg-box for this semigroup would contain infinitely many eggs, but all eggs are in the same box because there is only one D-class. (A semigroup for which all elements are D-related is called bisimple.)
It can be shown that within a D-class, all H-classes are the same size. For example, the transformation semigroup T4 contains four D-classes, within which the H-classes have 1, 2, 6, and 24 elements respectively.
Recent advances in the combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
of semigroups have used Green's relations to help enumerate semigroups with certain properties. A typical result (Satoh, Yama, and Tokizawa 1994) shows that there are exactly 1,843,120,128 non-equivalent semigroups of order 8, including 221,805 which are commutative; their work is based on a systematic exploration of possible D-classes. (By contrast, there are only five groups of order 8.)
Example
The full transformation semigroup T3 consists of all functions from the set {1, 2, 3} to itself; there are 27 of these. Write (a b c) for the function which sends 1 to a, 2 to b, and 3 to c. Since T3 contains the identity map, (1 2 3), there is no need to adjoin an identity.The egg-box diagram for T3 has three D-classes. They are also J-classes, because these relations coincide for a finite semigroup.
|
||||||||||
|
||||||||||
|
In T3, two functions are L-related if and only if they have the same image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
. Such functions appear in the same column of the table above. Likewise, the functions f and g are R-related if and only if
- f(x) = f(y) ⇔ g(x) = g(y)
for x and y in {1, 2, 3}; such functions are in the same table row. Consequently, two functions are D-related if and only if their images are the same size.
The elements in bold are the idempotents. Any H-class containing one of these is a (maximal) subgroup. In particular, the third D-class is isomorphic to the symmetric group S3. There are also six subgroups of order 2, and three of order 1 (as well as subgroups of these subgroups). Six elements of T3 are not in any subgroup.
Generalisations
There are essentially two ways of generalising an algebraic theory. One is to change its definitions so that it covers more or different objects; the other, more subtle way, is to find some desirable outcome of the theory and consider alternative ways of reaching that conclusion.Following the first route, analogous versions of Green's relations have been defined for semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
s (Grillet 1970) and rings (Petro 2002). Some, but not all, of the properties associated with the relations in semigroups carry over to these cases. Staying within the world of semigroups, Green's relations can be extended to cover relative ideals, which are subsets that are only ideals with respect to a subsemigroup (Wallace 1963).
For the second kind of generalisation, researchers have concentrated on properties of bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s between L- and R- classes. If x R y, then it is always possible to find bijections between Lx and Ly that are R-class-preserving. (That is, if two elements of an L-class are in the same R-class, then their images under a bijection will still be in the same R-class.) The dual statement for x L y also holds. These bijections are right and left translations, restricted to the appropriate equivalence classes. The question that arises is: how else could there be such bijections?
Suppose that Λ and Ρ are semigroups of partial transformations of some semigroup S. Under certain conditions, it can be shown that if x Ρ = y Ρ, with x ρ1 = y and y ρ2 = x, then the restrictions
- ρ1 : Λ x → Λ y
- ρ2 : Λ y → Λ x
are mutually inverse bijections. (Conventionally, arguments are written on the right for Λ, and on the left for Ρ.) Then the L and R relations can be defined by
- x L y if and only if Λ x = Λ y
- x R y if and only if x Ρ = y Ρ
and D and H follow as usual. Generalisation of J is not part of this system, as it plays no part in the desired property.
We call (Λ, Ρ) a Green's pair. There are several choices of partial transformation semigroup that yield the original relations. One example would be to take Λ to be the semigroup of all left translations on S1, restricted to S, and Ρ the corresponding semigroup of restricted right translations.
These definitions are due to Clark and Carruth (1980). They subsume Wallace's work, as well as various other generalised definitions proposed in the mid-1970s. The full axioms are fairly lengthy to state; informally, the most important requirements are that both Λ and Ρ should contain the identity transformation, and that elements of Λ should commute with elements of Ρ.