Graphical models for protein structure
Encyclopedia
Graphical model
s have become powerful frameworks for protein structure prediction
, protein–protein interaction and free energy
calculations for protein structures. Using a graphical model to represent the protein structure allows the solution of many problems including secondary structure prediction, protein protein interactions, protein-drug interaction, and free energy calculations.
There are two main approaches to use graphical models in protein structure modeling. The first approach uses discrete
variables for representing coordinates or dihedral angle
s of the protein structure. The variables are originally all continuous values and, to transform them into discrete values, a discretization process is typically applied. The second approach uses continuous variables for the coordinates or dihedral angles.
s X = (Xv)v ∈ V indexed by V, form a Markov random field with respect to G if they satisfy the pairwise Markov property:
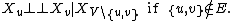
In the discrete model, the continuous variables are discretized into a set of favorable discrete values. If the variables of choice are dihedral angle
s, the discretization is typically done by mapping each value to the corresponding Rotamer conformation.
atoms, or equivalently, by a sequence of bond length
s and dihedral angle
s. The probability of a particular conformation
x can then be written as:
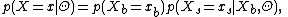
where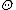
represents any parameters used to describe this model, including sequence information, temperature etc. Frequently the backbone is assumed to be rigid with a known conformation, and the problem is then transformed to a side-chain placement problem. The structure of the graph is also encoded in 
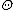. This structure shows which two variables are conditionally independent. As an example, side chain angles of two residues far apart can be independent given all other angles in the protein. To extract this structure, researchers use a distance threshold, and only pair of residues which are within that threshold are considered connected (i.e. have an edge between them).
Given this representation, the probability of a particular side chain conformation xs given the backbone conformation xb can be expressed as
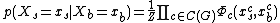
where C(G) is the set of all cliques in G,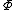
is a potential function
defined over the variables, and Z is the partition function
.
To completely characterize the MRF, it is necessary to define the potential function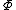
. To simplify, the cliques of a graph are usually restricted to only the cliques of size 2, which means the potential function is only defined over pairs of variables. In Goblin System, this pairwise functions are defined as
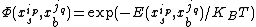
where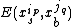
is the energy of interaction between rotamer state p of residue 
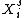and rotamer state q of residue 
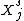and 
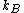is the Boltzmann constant.
Using a PDB file, this model can be built over the protein structure. From this model free energy can be calculated.
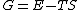
where E is the enthalpy of the system, T the temperature and S, the entropy. Now if we associate a probability with each state of the system, (p(x) for each conformation value, x), G can be rewritten as
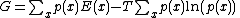
Calculating p(x) on discrete graphs is done by the generalized belief propagation algorithm. This algorithm calculates an approximation
to the probabilities, and it is not guaranteed to converge to a final value set. However, in practice, it has been shown to converge successfully in many cases.
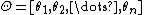be a set of 
variables, such as 
dihedral angles, and let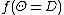 
be the value of the probability density function
at a particular value D. A multivariate Gaussian graphical model defines this probability as follows:
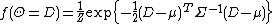
Where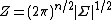
is the closed form for the partition function
. The parameters of this distribution are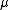
and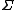 
. 
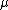is the vector of mean values of each variable, and 
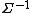, the inverse of the covariance matrix
, also known as the precision matrix. Precision matrix contains the pairwise dependencies between the variables. A zero value in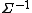
means that conditioned on the values of the other variables, the two corresponding variable are independent of each other.
To learn the graph structure as a multivariate Gaussian graphical model, we can use either L-1 regularization, or neghborhood selection algorithms. These algorithms simultaneously learn a graph structure and the edge strength of the connected nodes. An edge strength corresponds to the potential function defined on the corresponding two-node clique
. We use a training set of a number of PDB structures to learn the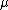
and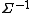 
.
Once the model is learned, we can repeat the same step as in the discrete case, to get the density functions at each node, and use analytical form to calculate the free energy. Here, the partition function
already has a closed form
, so the inference
, at least for the Gaussian graphical models is trivial. If the analytical form of the partition function is not available, particle filtering or expectation propagation
can be used to approximate Z, and then perform the inference and calculate free energy.
Graphical model
A graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
s have become powerful frameworks for protein structure prediction
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
, protein–protein interaction and free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
calculations for protein structures. Using a graphical model to represent the protein structure allows the solution of many problems including secondary structure prediction, protein protein interactions, protein-drug interaction, and free energy calculations.
There are two main approaches to use graphical models in protein structure modeling. The first approach uses discrete
Discrete
Discrete in science is the opposite of continuous: something that is separate; distinct; individual.Discrete may refer to:*Discrete particle or quantum in physics, for example in quantum theory...
variables for representing coordinates or dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
s of the protein structure. The variables are originally all continuous values and, to transform them into discrete values, a discretization process is typically applied. The second approach uses continuous variables for the coordinates or dihedral angles.
Discrete graphical models for protein structure
Markov random fields, also known as undirected graphical models are common representations for this problem. Given an undirected graph G = (V, E), a set of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X = (Xv)v ∈ V indexed by V, form a Markov random field with respect to G if they satisfy the pairwise Markov property:
- any two non-adjacent variables are conditionally independentConditional independenceIn probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
given all other variables:
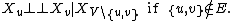
In the discrete model, the continuous variables are discretized into a set of favorable discrete values. If the variables of choice are dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
s, the discretization is typically done by mapping each value to the corresponding Rotamer conformation.
Model
Let X = {Xb, Xs} be the random variables representing the entire protein structure. Xb can be represented by a set of 3-d coordinates of the backboneBackbone
Backbone may refer to:* Vertebral column, of a vertebrate organism* Backbone chain, in polymer chemistry, the framework of the molecule* Backbone Entertainment, a video game development company* Backbone network, the top level of a hierarchical network...
atoms, or equivalently, by a sequence of bond length
Bond length
- Explanation :Bond length is related to bond order, when more electrons participate in bond formation the bond will get shorter. Bond length is also inversely related to bond strength and the bond dissociation energy, as a stronger bond will be shorter...
s and dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
s. The probability of a particular conformation
Protein structure
Proteins are an important class of biological macromolecules present in all organisms. Proteins are polymers of amino acids. Classified by their physical size, proteins are nanoparticles . Each protein polymer – also known as a polypeptide – consists of a sequence formed from 20 possible L-α-amino...
x can then be written as:
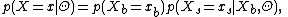
where
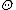represents any parameters used to describe this model, including sequence information, temperature etc. Frequently the backbone is assumed to be rigid with a known conformation, and the problem is then transformed to a side-chain placement problem. The structure of the graph is also encoded in 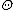. This structure shows which two variables are conditionally independent. As an example, side chain angles of two residues far apart can be independent given all other angles in the protein. To extract this structure, researchers use a distance threshold, and only pair of residues which are within that threshold are considered connected (i.e. have an edge between them).Given this representation, the probability of a particular side chain conformation xs given the backbone conformation xb can be expressed as
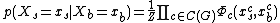
where C(G) is the set of all cliques in G,
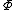is a potential functionPotential function
The term potential function may refer to:* A mathematical function whose values are a physical potential.* The class of functions known as harmonic functions, which are the topic of study in potential theory.* The potential function of a potential game....
defined over the variables, and Z is the partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
.
To completely characterize the MRF, it is necessary to define the potential function
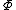. To simplify, the cliques of a graph are usually restricted to only the cliques of size 2, which means the potential function is only defined over pairs of variables. In Goblin System, this pairwise functions are defined as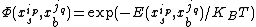where
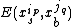is the energy of interaction between rotamer state p of residue 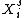and rotamer state q of residue 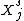and 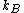is the Boltzmann constant.Using a PDB file, this model can be built over the protein structure. From this model free energy can be calculated.
Free energy calculation: belief propagation
It has been shown that the free energy of a system is calculated as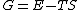where E is the enthalpy of the system, T the temperature and S, the entropy. Now if we associate a probability with each state of the system, (p(x) for each conformation value, x), G can be rewritten as
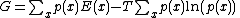
Calculating p(x) on discrete graphs is done by the generalized belief propagation algorithm. This algorithm calculates an approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
to the probabilities, and it is not guaranteed to converge to a final value set. However, in practice, it has been shown to converge successfully in many cases.
Continuous graphical models for protein structures
Graphical models can still be used when the variables of choice are continuous. In these cases, the probability distribution is represented as a multivariate probability distribution over continuous variables. Each family of distribution will then impose certain properties on the graphical model. Multivariate Gaussian distribution is one of the most convenient distributions in this problem. The simple form of the probability, and the direct relation with the corresponding graphical model makes it a popular choice among researchers.Gaussian graphical models of protein structures
Gaussian graphical models are multivariate probability distributions encoding a network of dependencies among variables. Let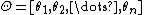 be a set of variables, such as dihedral angles, and let 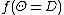be the value of the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
at a particular value D. A multivariate Gaussian graphical model defines this probability as follows:
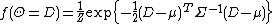
Where
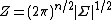is the closed form for the partition functionPartition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
. The parameters of this distribution are
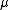and 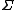. 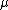is the vector of mean values of each variable, and 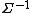, the inverse of the covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
, also known as the precision matrix. Precision matrix contains the pairwise dependencies between the variables. A zero value in
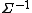means that conditioned on the values of the other variables, the two corresponding variable are independent of each other.To learn the graph structure as a multivariate Gaussian graphical model, we can use either L-1 regularization, or neghborhood selection algorithms. These algorithms simultaneously learn a graph structure and the edge strength of the connected nodes. An edge strength corresponds to the potential function defined on the corresponding two-node clique
Clique
A clique is an exclusive group of people who share common interests, views, purposes, patterns of behavior, or ethnicity. A clique as a reference group can be either normative or comparative. Membership in a clique is typically exclusive, and qualifications for membership may be social or...
. We use a training set of a number of PDB structures to learn the
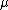and 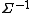.Once the model is learned, we can repeat the same step as in the discrete case, to get the density functions at each node, and use analytical form to calculate the free energy. Here, the partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
already has a closed form
Closed form
-Maths:* Closed-form expression, a finitary expression* Closed differential form, a differential form \alpha with the property that d\alpha = 0-Poetry:* In poetry analysis, a type of poetry that exhibits regular structure, such as meter or a rhyming pattern;...
, so the inference
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
, at least for the Gaussian graphical models is trivial. If the analytical form of the partition function is not available, particle filtering or expectation propagation
Expectation propagation
Expectation propagation is a technique in Bayesian machine learning, developed by Thomas Minka.EP finds approximations to a probability distribution. It uses an iterative approach that leverages the factorization structure of the target distribution. It differs from other Bayesian approximation...
can be used to approximate Z, and then perform the inference and calculate free energy.
External links
- http://www.liebertonline.com/doi/pdf/10.1089/cmb.2007.0131
- http://www.learningtheory.org/colt2008/81-Zhou.pdf