
Graph product
Encyclopedia
In mathematics
, a graph product is a certain kind of binary operation
on graph
s. Specifically, it is an operation that takes two graphs G1 and G2 and produces a graph H with the following properties:
The following table shows the most common graph products, with ∼ denoting “is connected by an edge to”:
In general, a graph product is determined by any condition for (u1, u2) ∼ (v1, v2) that can be expressed in terms of the statements u1 ∼ v1, u2 ∼ v2, u1 = v1, and u2 = v2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a graph product is a certain kind of binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
on graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s. Specifically, it is an operation that takes two graphs G1 and G2 and produces a graph H with the following properties:
- The vertex setVertex (graph theory)In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
of H is the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
V(G1) × V(G2), where V(G1) and V(G2) are the vertex sets of G1 and G2, respectively. - Two vertices (u1, u2) and (v1, v2) of H are connected by an edge if and only if the vertices u1, u2, v1, v2 satisfy conditions of a certain type (see below).
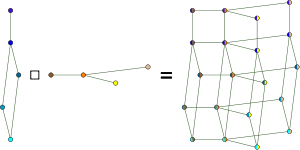
The following table shows the most common graph products, with ∼ denoting “is connected by an edge to”:
| Name | Condition for (u1, u2) ∼ (v1, v2). | Dimensions | Example |
|---|---|---|---|
| Cartesian product Cartesian product of graphs In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and... |
( u1 = v1 and u2 ∼ v2 ) or ( u1 ∼ v1 and u2 = v2 ) |
 |
 |
| Tensor product Tensor product of graphs In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and... |
u1 ∼ v1 and u2 ∼ v2 | 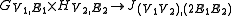 |
 |
| Lexicographical product | u1 ∼ v1 or ( u1 = v1 and u2 ∼ v2 ) |
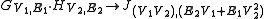 |
|
| Strong product Strong product of graphs In graph theory, the strong product G ⊠ H of graphs G and H is a graph such that* the vertex set of G ⊠ H is the Cartesian product V × V; and... (Normal product, AND product) |
( u1 = v1 and u2 ∼ v2 ) or ( u1 ∼ v1 and u2 = v2 ) or ( u1 ∼ v1 and u2 ∼ v2 ) |
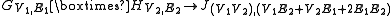 |
|
| Co-normal product (disjunctive product, OR product) |
u1 ∼ v1 or u2 ∼ v2 |
||
| Rooted product | see article | 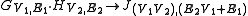 |
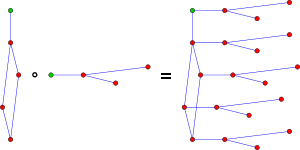 |
In general, a graph product is determined by any condition for (u1, u2) ∼ (v1, v2) that can be expressed in terms of the statements u1 ∼ v1, u2 ∼ v2, u1 = v1, and u2 = v2.

