
Graham's number
Encyclopedia
Graham's number, named after Ronald Graham
, is a large number
that is an upper bound on the solution to a certain problem in Ramsey theory
.
The number gained a degree of popular attention when Martin Gardner
described it in the "Mathematical Games" section of Scientific American in November 1977, writing that, "In an unpublished proof, Graham has recently established ... a bound so vast that it holds the record for the largest number ever used in a serious mathematical proof." The 1980 Guinness Book of World Records repeated Gardner's claim, adding to the popular interest in this number.
Graham's number is unimaginably larger than other well-known large numbers such as a googol
, googolplex, and even larger than Skewes' number and Moser's number. Indeed, the observable universe
is far too small to contain an ordinary digital representation
of Graham's number, assuming that each digit occupies at least one Planck volume. Even power towers
of the form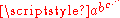 are useless for this purpose, although it can be easily described by recursive formulas using Knuth's up-arrow notation
are useless for this purpose, although it can be easily described by recursive formulas using Knuth's up-arrow notation
or the equivalent, as was done by Graham. The last ten digits of Graham's number are ...2464195387.
Specific integers known to be far larger than Graham's number have since appeared in many serious mathematical proofs (e.g., in connection with Friedman's various finite forms of Kruskal's theorem).
:
Graham & Rothschild (1971) proved that this problem has a solution, N*, and gave as a bounding estimate 6 ≤ N* ≤ N, with the upper bound N a particular, explicitly defined, very large number. (In terms of Knuth up-arrow notation, , where
, where  .) The lower bound of 6 was later improved to 11 by Geoff Exoo of Indiana State University (2003) and even further to 13 by Jerome Barkley in 2008. Thus, the best known explicit bounding estimate for the solution N* is now 13 ≤ N* ≤ N.
.) The lower bound of 6 was later improved to 11 by Geoff Exoo of Indiana State University (2003) and even further to 13 by Jerome Barkley in 2008. Thus, the best known explicit bounding estimate for the solution N* is now 13 ≤ N* ≤ N.
The subject of the present article is an upper bound G that's much weaker (larger) than N; namely,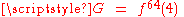 , where
, where 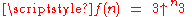 . This weaker upper bound, attributed to some unpublished work of Graham, was eventually published (and dubbed Graham's number) by Martin Gardner, in [Scientific American, "Mathematical Games", November 1977].
. This weaker upper bound, attributed to some unpublished work of Graham, was eventually published (and dubbed Graham's number) by Martin Gardner, in [Scientific American, "Mathematical Games", November 1977].
, Graham's number G (as defined in Gardner's Scientific American article) is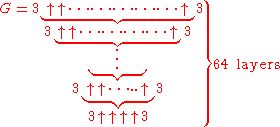
where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,
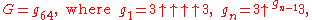
and where a superscript on an up-arrow indicates how many arrows are there. In other words, G is calculated in 64 steps: the first step is to calculate g1 with four up-arrows between 3s; the second step is to calculate g2 with g1 up-arrows between 3's; the third step is to calculate g3 with g2 up-arrows between 3's; and so on, until finally calculating G = g64 with g63 up-arrows between 3s.
Equivalently,
and the superscript on f indicates an iteration of the function
, e.g., f 4(n) = f(f(f(f(n)))). Expressed in terms of the family of hyperoperation
s , the function f is the particular sequence
, the function f is the particular sequence 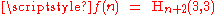 , which is a version of the rapidly-growing the Ackermann function
, which is a version of the rapidly-growing the Ackermann function
A(n,n). (In fact,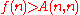 for all n.) The function f can also be expressed in Conway chained arrow notation as
for all n.) The function f can also be expressed in Conway chained arrow notation as  , and this notation also provides the following bounds on G:
, and this notation also provides the following bounds on G:
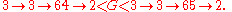
(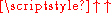 ) alone:
) alone:
where the number of 3s in the expression on the right is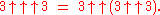
Now each tetration
( ) operation reduces to a "tower" of exponentiations (
) operation reduces to a "tower" of exponentiations ( ) according to the definition
) according to the definition
Thus,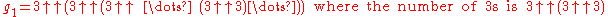
becomes, solely in terms of repeated "exponentiation towers",
and where the number of 3s in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right.
In other words, g1 is computed by first calculating the number of towers, n = 3↑3↑3↑...↑3 (where the number of 3s is 3↑3↑3 = 7625597484987), and then computing the nth tower in the following sequence:
1st tower: 3
2nd tower: 3↑3↑3 (number of 3s is 3) = 7625597484987
3rd tower: 3↑3↑3↑3↑...↑3 (number of 3s is 7625597484987) = ...
.
.
.
g1 = nth tower: 3↑3↑3↑3↑3↑3↑3↑...↑3 (number of 3s is given by the n-1th tower)
where the number of 3s in each successive tower is given by the tower just before it. Note that the result of calculating the third tower is the value of n, the number of towers for g1.
The magnitude of this first term, g1, is so large that it is practically incomprehensible, even though the above display is relatively easy to comprehend. Even n, the mere number of towers in this formula for g1, is far greater than the number of Planck volume
s (roughly 10185 of them) into which one can imagine subdividing the observable universe
. And after this first term, still another 63 terms remain in the rapidly growing g sequence before Graham's number G = g64 is reached.
 n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost "3" in the tower; i.e., the topmost "3" can be changed to any other nonnegative integer without affecting the d rightmost digits.
n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost "3" in the tower; i.e., the topmost "3" can be changed to any other nonnegative integer without affecting the d rightmost digits.
The following table illustrates, for a few values of d, how this happens. For a given height of tower and number of digits d, the full range of d-digit numbers (10d of them) does not occur; instead, a certain smaller subset of values repeats itself in a cycle. The length of the cycle and some of the values (in parentheses) are shown in each cell of this table:
The particular rightmost d digits that are ultimately shared by all sufficiently tall towers of 3s are in bold text, and can be seen developing as the tower height increases. For any fixed number of digits d (row in the table), the number of values possible for 3 3
3 ...3
...3 x mod 10d, as x ranges over all nonnegative integers, is seen to decrease steadily as the height increases, until eventually reducing the "possibility set" to a single number (colored cells) when the height exceeds d+2.
x mod 10d, as x ranges over all nonnegative integers, is seen to decrease steadily as the height increases, until eventually reducing the "possibility set" to a single number (colored cells) when the height exceeds d+2.
A simple algorithm for computing these digits may be described as follows: let x = 3, then iterate, d times, the assignment
x = 3x mod 10d. Except for omitting any leading 0s, the final value assigned to x (as a base-ten numeral) is then composed of the d rightmost decimal digits of 3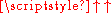 n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.)
n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.)
This algorithm produces the following 500 rightmost decimal digits of Graham's number (or any tower of more than 500 3s):
...02425950695064738395657479136519351798334535362521
43003540126026771622672160419810652263169355188780
38814483140652526168785095552646051071172000997092
91249544378887496062882911725063001303622934916080
25459461494578871427832350829242102091825896753560
43086993801689249889268099510169055919951195027887
17830837018340236474548882222161573228010132974509
27344594504343300901096928025352751833289884461508
94042482650181938515625357963996189939679054966380
03222348723967018485186439059104575627262464195387.
Ronald Graham
Ronald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
, is a large number
Large numbers
This article is about large numbers in the sense of numbers that are significantly larger than those ordinarily used in everyday life, for instance in simple counting or in monetary transactions...
that is an upper bound on the solution to a certain problem in Ramsey theory
Ramsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
.
The number gained a degree of popular attention when Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
described it in the "Mathematical Games" section of Scientific American in November 1977, writing that, "In an unpublished proof, Graham has recently established ... a bound so vast that it holds the record for the largest number ever used in a serious mathematical proof." The 1980 Guinness Book of World Records repeated Gardner's claim, adding to the popular interest in this number.
Graham's number is unimaginably larger than other well-known large numbers such as a googol
Googol
A googol is the large number 10100, that is, the digit 1 followed by 100 zeros:The term was coined in 1938 by 9-year-old Milton Sirotta , nephew of American mathematician Edward Kasner...
, googolplex, and even larger than Skewes' number and Moser's number. Indeed, the observable universe
Observable universe
In Big Bang cosmology, the observable universe consists of the galaxies and other matter that we can in principle observe from Earth in the present day, because light from those objects has had time to reach us since the beginning of the cosmological expansion...
is far too small to contain an ordinary digital representation
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
of Graham's number, assuming that each digit occupies at least one Planck volume. Even power towers
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
of the form
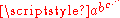 are useless for this purpose, although it can be easily described by recursive formulas using Knuth's up-arrow notation
are useless for this purpose, although it can be easily described by recursive formulas using Knuth's up-arrow notationKnuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
or the equivalent, as was done by Graham. The last ten digits of Graham's number are ...2464195387.
Specific integers known to be far larger than Graham's number have since appeared in many serious mathematical proofs (e.g., in connection with Friedman's various finite forms of Kruskal's theorem).
Graham's problem
Graham's number is connected to the following problem in the branch of mathematics known as Ramsey theoryRamsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
:
- Consider an n-dimensional hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
, and connect each pair of verticesVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
to obtain a complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on 2n verticesVertex (graph theory)In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
. Then colour each of the edges of this graph either red or blue. - What is the smallest value of n for which every such colouring contains at least one single-coloured 4-vertex planarPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
complete subgraph?
Graham & Rothschild (1971) proved that this problem has a solution, N*, and gave as a bounding estimate 6 ≤ N* ≤ N, with the upper bound N a particular, explicitly defined, very large number. (In terms of Knuth up-arrow notation,
 , where
, where  .) The lower bound of 6 was later improved to 11 by Geoff Exoo of Indiana State University (2003) and even further to 13 by Jerome Barkley in 2008. Thus, the best known explicit bounding estimate for the solution N* is now 13 ≤ N* ≤ N.
.) The lower bound of 6 was later improved to 11 by Geoff Exoo of Indiana State University (2003) and even further to 13 by Jerome Barkley in 2008. Thus, the best known explicit bounding estimate for the solution N* is now 13 ≤ N* ≤ N.The subject of the present article is an upper bound G that's much weaker (larger) than N; namely,
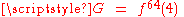 , where
, where 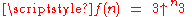 . This weaker upper bound, attributed to some unpublished work of Graham, was eventually published (and dubbed Graham's number) by Martin Gardner, in [Scientific American, "Mathematical Games", November 1977].
. This weaker upper bound, attributed to some unpublished work of Graham, was eventually published (and dubbed Graham's number) by Martin Gardner, in [Scientific American, "Mathematical Games", November 1977].Definition of Graham's number
Using Knuth's up-arrow notationKnuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
, Graham's number G (as defined in Gardner's Scientific American article) is

where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,
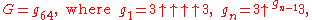
and where a superscript on an up-arrow indicates how many arrows are there. In other words, G is calculated in 64 steps: the first step is to calculate g1 with four up-arrows between 3s; the second step is to calculate g2 with g1 up-arrows between 3's; the third step is to calculate g3 with g2 up-arrows between 3's; and so on, until finally calculating G = g64 with g63 up-arrows between 3s.
Equivalently,

and the superscript on f indicates an iteration of the function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
, e.g., f 4(n) = f(f(f(f(n)))). Expressed in terms of the family of hyperoperation
Hyperoperation
In mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
s
 , the function f is the particular sequence
, the function f is the particular sequence 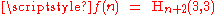 , which is a version of the rapidly-growing the Ackermann function
, which is a version of the rapidly-growing the Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
A(n,n). (In fact,
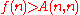 for all n.) The function f can also be expressed in Conway chained arrow notation as
for all n.) The function f can also be expressed in Conway chained arrow notation as  , and this notation also provides the following bounds on G:
, and this notation also provides the following bounds on G: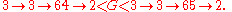
Magnitude of Graham's number
To convey the difficulty of appreciating the enormous size of Graham's number, it may be helpful to express—in terms of exponentiation alone—just the first term (g1) of the rapidly growing 64-term sequence. First, in terms of tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
(
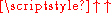 ) alone:
) alone:
where the number of 3s in the expression on the right is
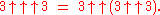
Now each tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
(
 ) operation reduces to a "tower" of exponentiations (
) operation reduces to a "tower" of exponentiations ( ) according to the definition
) according to the definition
Thus,
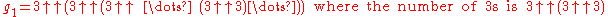
becomes, solely in terms of repeated "exponentiation towers",

and where the number of 3s in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right.
In other words, g1 is computed by first calculating the number of towers, n = 3↑3↑3↑...↑3 (where the number of 3s is 3↑3↑3 = 7625597484987), and then computing the nth tower in the following sequence:
1st tower: 3
2nd tower: 3↑3↑3 (number of 3s is 3) = 7625597484987
3rd tower: 3↑3↑3↑3↑...↑3 (number of 3s is 7625597484987) = ...
.
.
.
g1 = nth tower: 3↑3↑3↑3↑3↑3↑3↑...↑3 (number of 3s is given by the n-1th tower)
where the number of 3s in each successive tower is given by the tower just before it. Note that the result of calculating the third tower is the value of n, the number of towers for g1.
The magnitude of this first term, g1, is so large that it is practically incomprehensible, even though the above display is relatively easy to comprehend. Even n, the mere number of towers in this formula for g1, is far greater than the number of Planck volume
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
s (roughly 10185 of them) into which one can imagine subdividing the observable universe
Observable universe
In Big Bang cosmology, the observable universe consists of the galaxies and other matter that we can in principle observe from Earth in the present day, because light from those objects has had time to reach us since the beginning of the cosmological expansion...
. And after this first term, still another 63 terms remain in the rapidly growing g sequence before Graham's number G = g64 is reached.
Rightmost decimal digits of Graham's number
Graham's number is a "power tower" of the form 3 n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost "3" in the tower; i.e., the topmost "3" can be changed to any other nonnegative integer without affecting the d rightmost digits.
n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost "3" in the tower; i.e., the topmost "3" can be changed to any other nonnegative integer without affecting the d rightmost digits.The following table illustrates, for a few values of d, how this happens. For a given height of tower and number of digits d, the full range of d-digit numbers (10d of them) does not occur; instead, a certain smaller subset of values repeats itself in a cycle. The length of the cycle and some of the values (in parentheses) are shown in each cell of this table:
| Number of digits (d) | | 3 x x | | 3 3 3 x x | | 3 3 3 3 3 x x | | 3 3 3 3 3 3 3 x x | | 3 3 3 3 3 3 3 3 3 x x |
|---|---|---|---|---|---|
| 1 | 4 (1,3,9,7) |
2 (3,7) |
1 (7) |
1 (7) |
1 (7) |
| 2 | 20 (01,03,...,87,...,67) |
4 (03,27,83,87) |
2 (27,87) |
1 (87) |
1 (87) |
| 3 | 100 (001,003,...,387,...,667) |
20 (003,027,...387,...,587) |
4 (027,987,227,387) |
2 (987,387) |
1 (387) |
The particular rightmost d digits that are ultimately shared by all sufficiently tall towers of 3s are in bold text, and can be seen developing as the tower height increases. For any fixed number of digits d (row in the table), the number of values possible for 3
 3
3 ...3
...3 x mod 10d, as x ranges over all nonnegative integers, is seen to decrease steadily as the height increases, until eventually reducing the "possibility set" to a single number (colored cells) when the height exceeds d+2.
x mod 10d, as x ranges over all nonnegative integers, is seen to decrease steadily as the height increases, until eventually reducing the "possibility set" to a single number (colored cells) when the height exceeds d+2.A simple algorithm for computing these digits may be described as follows: let x = 3, then iterate, d times, the assignment
Assignment (computer science)
In computer programming, an assignment statement sets or re-sets the value stored in the storage location denoted by a variable name. In most imperative computer programming languages, assignment statements are one of the basic statements...
x = 3x mod 10d. Except for omitting any leading 0s, the final value assigned to x (as a base-ten numeral) is then composed of the d rightmost decimal digits of 3
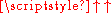 n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.)
n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.)This algorithm produces the following 500 rightmost decimal digits of Graham's number (or any tower of more than 500 3s):
...02425950695064738395657479136519351798334535362521
43003540126026771622672160419810652263169355188780
38814483140652526168785095552646051071172000997092
91249544378887496062882911725063001303622934916080
25459461494578871427832350829242102091825896753560
43086993801689249889268099510169055919951195027887
17830837018340236474548882222161573228010132974509
27344594504343300901096928025352751833289884461508
94042482650181938515625357963996189939679054966380
03222348723967018485186439059104575627262464195387.
External links
- "A Ramsey Problem on Hypercubes" by Geoff Exoo
- Mathworld article on Graham's number
- How to calculate Graham's number
- Some Ramsey results for the n-cube prepublication mentions Graham's number


 3
3 ...3
...3 x when all but the rightmost d decimal digits are ignored
x when all but the rightmost d decimal digits are ignored