Goldbeter-Koshland kinetics
Encyclopedia
The Goldbeter-Koshland kinetics describe a steady-state solution
for a 2-state biological system. In this system, the interconversion between these two states is performed by two enzyme
s with opposing effect. One example would be a protein Z that exists in a phosphorylated
form ZP and in an unphosphorylated form Z; the corresponding kinase
Y and phosphatase
X interconvert the two forms. In this case we would be interested in the equilibrium concentration of the protein Z (Goldbeter-Koshland kinetics only describe equilibrium properties, thus no dynamics can be modeled). It has many applications in the description of biological systems.
The Goldbeter-Koshland kinetics is described by the Goldbeter-Koshland function:
Steady state (chemistry)
In chemistry, a steady state is a situation in which all state variables are constant in spite of ongoing processes that strive to change them. For an entire system to be at steady state, i.e. for all state variables of a system to be constant, there must be a flow through the system...
for a 2-state biological system. In this system, the interconversion between these two states is performed by two enzyme
Enzyme
Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...
s with opposing effect. One example would be a protein Z that exists in a phosphorylated
Phosphorylation
Phosphorylation is the addition of a phosphate group to a protein or other organic molecule. Phosphorylation activates or deactivates many protein enzymes....
form ZP and in an unphosphorylated form Z; the corresponding kinase
Kinase
In chemistry and biochemistry, a kinase is a type of enzyme that transfers phosphate groups from high-energy donor molecules, such as ATP, to specific substrates, a process referred to as phosphorylation. Kinases are part of the larger family of phosphotransferases...
Y and phosphatase
Phosphatase
A phosphatase is an enzyme that removes a phosphate group from its substrate by hydrolysing phosphoric acid monoesters into a phosphate ion and a molecule with a free hydroxyl group . This action is directly opposite to that of phosphorylases and kinases, which attach phosphate groups to their...
X interconvert the two forms. In this case we would be interested in the equilibrium concentration of the protein Z (Goldbeter-Koshland kinetics only describe equilibrium properties, thus no dynamics can be modeled). It has many applications in the description of biological systems.
The Goldbeter-Koshland kinetics is described by the Goldbeter-Koshland function:
-
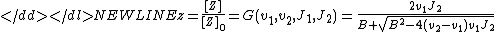
with the constants-
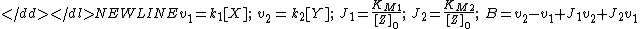
Graphically the function takes values between 0 and 1 and has a sigmoidSigmoid functionMany natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
behavior. The smaller the parameters J1 and J2 the steeper the function gets and the more of a switch-like behavior is observed.
Derivation
Since we are looking at equilibrium properties we can write-
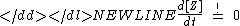
From Michaelis–Menten kinetics we know that the rate at which ZP is dephosphorylated is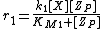
and the rate at which Z is phosphorylated is 
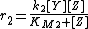. Here the KM stand for the Michaelis Menten constant which describes how well the enzymes X and Y bind and catalyze the conversion whereas the kinetic parameters k1 and k2 denote the rate constants for the catalyzed reactions. Assuming that the total concentration of Z is constant we can additionally write that [Z]0 = [ZP] + [Z] and we thus get:
-
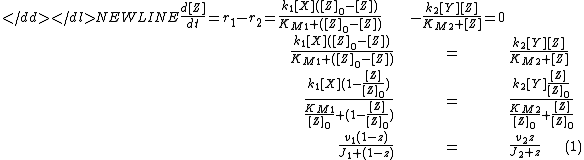
with the constants-
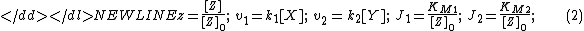
If we thus solve the quadratic equationQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
(1) for z we get:-
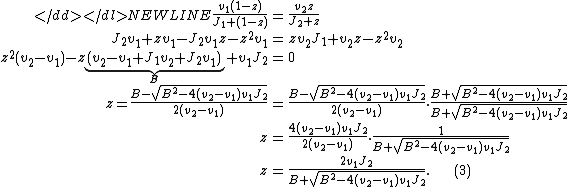
Thus (3) is a solution to the initial equilibrium problem and describes the equilibrium concentration of [Z] and [ZP] as a function of the kinetic parameters of the phoshorylation and dephoshorylation reaction and the concentrations of the kinase and phosphotase. The solution is the Goldbeter-Koshland function with the constants from (2):-
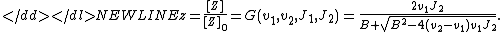
Literature
- Zoltan Szallasi, Jörg Stelling, Vipul Periwal: System Modeling in Cellular Biology. The MIT Press. p 108. ISBN 978-0262195485
-
-
-
-
-
-