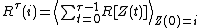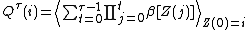Gittins index
Encyclopedia
The Gittins index is a measure of the reward that can be achieved by a process evolving from its present state onwards with the probability that it will be terminated in future. It is a real
scalar
value associated to the state of a stochastic process
with a reward function and with a probability of termination.
If we were to make a judgment call at that early time in development we could be condemning one technology to being put on the shelf and the other would be developed and put into operation. If we develop both technologies we would be able to make a judgment call on each by comparing the progress of each technology at a set time interval such as every three months. The decisions we make about investment in the next stage would be based on those results.
In a paper in 1979 called Bandit Processes and Dynamic Allocation Indices John C. Gittins
suggests a solution for problems such as this. He takes the two basic functions of a "Scheduling Problem" and a "Multi-armed bandit" problem and shows how these problems can be solved using Dynamic allocation indices. He first takes the "Scheduling Problem" and reduces it to a machine which has to perform jobs and has a set time period, every hour or day for example, to finish each job in. The machine is given a reward value, based on finishing or not within the time period, and a probability value of whether it will finish or not for each job is calculated. The problem is "to decide which job to process next at each stage so as to maximize the total expected reward." He then moves on to the "Multi–armed bandit problem" where each pull on a "one armed bandit
" lever is allocated a reward function for a successful pull, and a zero reward for an unsuccessful pull. The sequence of successes forms a Bernoulli process and has an unknown probability of success. There are multiple "bandits" and the distribution of successful pulls is calculated and different for each machine. Gittins states that the problem here is "to decide which arm to pull next at each stage so as to maximize the total expected reward from an infinite sequence of pulls."
Gittins says that "Both the problems described above involve a sequence of decisions, each of which is based on more information than its predecessors, and this both problems may be tackled by dynamic allocation indices."
scalar
value associated to the state of a stochastic process
with a reward function and with a probability of termination. It is a measure of the reward that can be achieved by the process evolving from that state on, under the probability that it will be terminated in future. The "index policy" induced by the Gittins index, consisting of choosing at any time the stochastic process with the currently highest Gittins index, is the solution of some stopping problems
such as the one of dynamic allocation, where a decision-maker has to maximize the total reward by distributing a limited amount of effort to a number of competing projects, each returning a stochastic reward. If the projects are independent from each other and only one project at a time may evolve, the problem is called multi-armed bandit
and the Gittins index policy is optimal. If multiple projects can evolve, the problem is called Restless bandit and the Gittins index policy is a known good heuristic but no optimal solution exists in general. In fact, in general this problem is NP-complex
and it is generally accepted that no feasible solution can be found.
Soon after the seminal paper of Gittins, Peter Whittle
demonstrated that the index emerges as a lagrangian multiplier from a dynamic programming formulation of the problem called retirement process and conjectured that the same index would be a good heuristic in a more general setup named Restless bandit. The question of how to actually calculate the index has been solved for Markov chain
s in the 1980s by Varaiya and his collaborators with an algorithm that computes the indexes
from the largest first down to the smallest. Katehakis and Veinot demonstrated that the index is the expected reward of a Markov decision process
constructed over the Markov chain and known as Restart in State and can be calculated exactly by solving that problem with the policy iteration algorithm, or approximately with the value iteration algorithm.
This approach has the advantage of calculating the index for one specific state without having to calculate all the greater indexes. A faster algorithm for the calculation of the indexes has been obtained in 2004 by Sonin as a consequence of his elimination algorithm for the optimal stopping of a Markov chain. In this algorithm the termination probability of the process may depend on the current state rather than being a fixed factor. A faster algorithm has been proposed in 2007 by Niño-Mora by exploting the structure of a parametric simplex to reduce the computational effort of the pivot steps and thereby achieving the same complexity as the gaussian elimination algorithm.
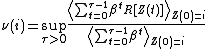
where
is a stochastic process, 
is the
utility (also called reward) associated to the discrete state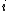
,
is the probability that the stochastic process does not
terminate, and
is the conditional expectation
operator given c:
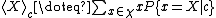
with
being the range
of X.
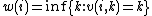
where
is the value function
with the same notation as above. It holds that
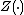is a Markov chain with rewards, the interpretation of Katehakis and Veinott (1987) associates to every state the action of restarting from one arbitrary state 
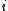, thereby constructing a Markov decision process 
.
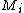The Gittins Index of that state
is the highest total reward which can be achieved on 
if one can always choose to continue or restart from that state 
.
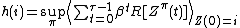
where
indicates a policy over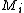 
. It holds that
.
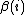depends on the state 
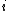, a generalization introduced by Sonin (2008) defines the Gittins index 
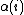as the maximum discounted total reward per chance of termination.
where
If
is replaced by 
in the definitions of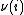 
, 
and 
, then it holds that
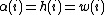
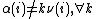
this observation leads Sonin to conclude that
and not 
is the true meaning of the Gittins index.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
value associated to the state of a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with a reward function and with a probability of termination.
Terminology
To illustrate the theory we can take two examples from a developing sector, such as from electricity generating technologies: wind power and wave power. If we are presented with the two technologies when they are both proposed as ideas we cannot say which will be better in the long run as we have no data, as yet, to base our judgments on. It would be easy to say that wave power would be too problematic to develop as it seems easier to put up lots of wind turbines than to make the long floating generators, tow them out to sea and lay the cables necessary.If we were to make a judgment call at that early time in development we could be condemning one technology to being put on the shelf and the other would be developed and put into operation. If we develop both technologies we would be able to make a judgment call on each by comparing the progress of each technology at a set time interval such as every three months. The decisions we make about investment in the next stage would be based on those results.
In a paper in 1979 called Bandit Processes and Dynamic Allocation Indices John C. Gittins
John C. Gittins
John C. Gittins is a researcher in applied probability and operations research, who is a professor and Emeritus Fellow at Keble College, Oxford University....
suggests a solution for problems such as this. He takes the two basic functions of a "Scheduling Problem" and a "Multi-armed bandit" problem and shows how these problems can be solved using Dynamic allocation indices. He first takes the "Scheduling Problem" and reduces it to a machine which has to perform jobs and has a set time period, every hour or day for example, to finish each job in. The machine is given a reward value, based on finishing or not within the time period, and a probability value of whether it will finish or not for each job is calculated. The problem is "to decide which job to process next at each stage so as to maximize the total expected reward." He then moves on to the "Multi–armed bandit problem" where each pull on a "one armed bandit
Slot machine
A slot machine , informally fruit machine , the slots , poker machine or "pokies" or simply slot is a casino gambling machine with three or more reels which spin when a button is pushed...
" lever is allocated a reward function for a successful pull, and a zero reward for an unsuccessful pull. The sequence of successes forms a Bernoulli process and has an unknown probability of success. There are multiple "bandits" and the distribution of successful pulls is calculated and different for each machine. Gittins states that the problem here is "to decide which arm to pull next at each stage so as to maximize the total expected reward from an infinite sequence of pulls."
Gittins says that "Both the problems described above involve a sequence of decisions, each of which is based on more information than its predecessors, and this both problems may be tackled by dynamic allocation indices."
Definition
In applied mathematics, the "Gittins index" is a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
value associated to the state of a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with a reward function and with a probability of termination. It is a measure of the reward that can be achieved by the process evolving from that state on, under the probability that it will be terminated in future. The "index policy" induced by the Gittins index, consisting of choosing at any time the stochastic process with the currently highest Gittins index, is the solution of some stopping problems
Optimal stopping
In mathematics, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance...
such as the one of dynamic allocation, where a decision-maker has to maximize the total reward by distributing a limited amount of effort to a number of competing projects, each returning a stochastic reward. If the projects are independent from each other and only one project at a time may evolve, the problem is called multi-armed bandit
Multi-armed bandit
In statistics, particularly in the design of sequential experiments, a multi-armed bandit takes its name from a traditional slot machine . Multiple levers are considered in the motivating applications in statistics. When pulled, each lever provides a reward drawn from a distribution associated...
and the Gittins index policy is optimal. If multiple projects can evolve, the problem is called Restless bandit and the Gittins index policy is a known good heuristic but no optimal solution exists in general. In fact, in general this problem is NP-complex
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
and it is generally accepted that no feasible solution can be found.
History
Questions about the optimal stopping policies in the context of clinical trials have been open from the 1940s and in the 1960s a few authors analyzed simple models leading to optimal index policies, but it was only in the 1970s that Gittins and his collaborators demonstrated in a markovian framework that the optimal solution of the general case is an index policy whose "dynamic allocation index" is computable in principle for every state of each project as a function of the single project's dynamics.Soon after the seminal paper of Gittins, Peter Whittle
Peter Whittle
Peter Whittle is a mathematician and statistician, working in the fields of stochastic nets, optimal control, time series analysis, stochastic optimization and stochastic dynamics...
demonstrated that the index emerges as a lagrangian multiplier from a dynamic programming formulation of the problem called retirement process and conjectured that the same index would be a good heuristic in a more general setup named Restless bandit. The question of how to actually calculate the index has been solved for Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s in the 1980s by Varaiya and his collaborators with an algorithm that computes the indexes
from the largest first down to the smallest. Katehakis and Veinot demonstrated that the index is the expected reward of a Markov decision process
Markov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
constructed over the Markov chain and known as Restart in State and can be calculated exactly by solving that problem with the policy iteration algorithm, or approximately with the value iteration algorithm.
This approach has the advantage of calculating the index for one specific state without having to calculate all the greater indexes. A faster algorithm for the calculation of the indexes has been obtained in 2004 by Sonin as a consequence of his elimination algorithm for the optimal stopping of a Markov chain. In this algorithm the termination probability of the process may depend on the current state rather than being a fixed factor. A faster algorithm has been proposed in 2007 by Niño-Mora by exploting the structure of a parametric simplex to reduce the computational effort of the pivot steps and thereby achieving the same complexity as the gaussian elimination algorithm.
Dynamic allocation index
The classical definition by Gittins et al. is: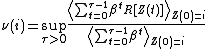where
is a stochastic process, is theutility (also called reward) associated to the discrete state
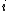, is the probability that the stochastic process does notterminate, and
is the conditional expectationoperator given c:
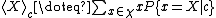
with
being the rangeRange (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of X.
Retirement process formulation
The dynamic programming formulation in terms of retirement process, given by Whittle, is: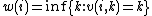where
is the value functionwith the same notation as above. It holds that
Restart-in-state formulation
If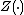 is a Markov chain with rewards, the interpretation of Katehakis and Veinott (1987) associates to every state the action of restarting from one arbitrary state 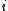, thereby constructing a Markov decision process 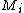.The Gittins Index of that state
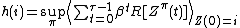
is the highest total reward which can be achieved on if one can always choose to continue or restart from that state .where
indicates a policy over 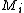. It holds that.Generalized index
If the probability of termination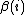 depends on the state 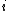, a generalization introduced by Sonin (2008) defines the Gittins index 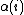as the maximum discounted total reward per chance of termination.where
If
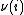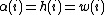
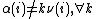
is replaced by in the definitions of , and , then it holds thatthis observation leads Sonin to conclude that
and not is the true meaning of the Gittins index.External links
- http://sites.google.com/site/lorenzodigregorio/gittins-index Matlab/Octave implementation of the index computation algorithms
- Bertsimas, D. and Niño-Mora, J. (1996). Conservation laws, extended polymatroids and multiarmed bandit problems: a polyhedral approach to indexable systems. Math. Oper. Res. 29 (1), 162–181.