Multi-armed bandit
Encyclopedia
In statistics, particularly in the design
of sequential experiments
, a multi-armed bandit takes its name from a traditional slot machine
(one-armed bandit). Multiple levers are considered in the motivating applications in statistics. When pulled, each lever provides a reward drawn from a distribution associated with that specific lever. The objective of the gambler is to maximize the sum of rewards earned through a sequence of lever pulls.Berry and Fristedt (1985)
In practice, multi-armed bandits have been used to model the problem of managing research projects in a large organization, like a science foundation or a pharmaceutical company. Given its fixed budget, the problem is to allocate resources among the competing projects, whose properties are only partially known now but may be better understood as time passes.
In the early versions of the multi-armed bandit problem, the gambler has no initial knowledge about the levers. The crucial tradeoff the gambler faces at each trial is between "exploitation" of the lever that has the highest expected payoff and "exploration" to get more information
about the expected payoffs of the other levers.
The multi-armed bandit is sometimes called a
-armed bandit or 
-armed bandit.
In these practical examples, the problem requires balancing reward maximization based on the knowledge already acquired with attempting new actions to further increase knowledge. This is known as the exploitation vs. exploration tradeoff in reinforcement learning
.
The model can also be used to control dynamic allocation of resources to different projects, answering the question "which project should I work on" given uncertainty about the difficulty and payoff of each possibility.
Originally considered by Allied scientists in World War II
, it proved so intractable that it was proposed the problem be dropped over Germany so that German scientists could also waste their time on it. It was formulated by Herbert Robbins
in 1952.
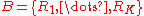, each distribution being associated with the rewards delivered by one of the K levers. Let 
be the mean values associated with these reward distributions. The gambler iteratively plays one lever per round and observes the associated reward. The objective is to maximize the sum of the collected rewards. The horizon H is the number of rounds that remain to be played. The bandit problem is formally equivalent to a one-state Markov decision process
. The regret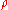
after T rounds is defined as the difference between the reward sum associated with an optimal strategy and the sum of the collected rewards: 
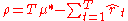, where 
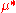is the maximal reward mean, 
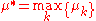, and 
is the reward at time t. A strategy whose average regret per round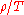 
tends to zero with probability 1 when the number of played rounds tends to infinity is a zero-regret strategy. Intuitively, zero-regret strategies are guaranteed to converge to an optimal strategy, not necessarily unique, if enough rounds are played.
Computer science researchers have studied multi-armed bandits under worst-case assumptions, obtaining positive results for
finite numbers of trials with both
stochastic and nonstochastic arm payoffs.
behavior where the best lever (based on previous observations) is always pulled except when a (uniformly) random action is taken.
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
of sequential experiments
Sequential analysis
In statistics, sequential analysis or sequential hypothesis testing is statistical analysis where the sample size is not fixed in advance. Instead data are evaluated as they are collected, and further sampling is stopped in accordance with a pre-defined stopping rule as soon as significant results...
, a multi-armed bandit takes its name from a traditional slot machine
Slot machine
A slot machine , informally fruit machine , the slots , poker machine or "pokies" or simply slot is a casino gambling machine with three or more reels which spin when a button is pushed...
(one-armed bandit). Multiple levers are considered in the motivating applications in statistics. When pulled, each lever provides a reward drawn from a distribution associated with that specific lever. The objective of the gambler is to maximize the sum of rewards earned through a sequence of lever pulls.Berry and Fristedt (1985)
In practice, multi-armed bandits have been used to model the problem of managing research projects in a large organization, like a science foundation or a pharmaceutical company. Given its fixed budget, the problem is to allocate resources among the competing projects, whose properties are only partially known now but may be better understood as time passes.
In the early versions of the multi-armed bandit problem, the gambler has no initial knowledge about the levers. The crucial tradeoff the gambler faces at each trial is between "exploitation" of the lever that has the highest expected payoff and "exploration" to get more information
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
about the expected payoffs of the other levers.
The multi-armed bandit is sometimes called a
-armed bandit or -armed bandit.Empirical motivation
The multi-armed bandit problem models an agent that simultaneously attempts to acquire new knowledge and to optimize its decisions based on existing knowledge. There are many practical applications:- clinical trialClinical trialClinical trials are a set of procedures in medical research and drug development that are conducted to allow safety and efficacy data to be collected for health interventions...
s investigating the effects of different experimental treatments while minimizing patient losses, and - adaptive routingAdaptive routingAdaptive routing describes the capability of a system, through which routes are characterized by their destination, to alter the path that the route takes through the system in response to a change in conditions...
efforts for minimizing delays in a network.
In these practical examples, the problem requires balancing reward maximization based on the knowledge already acquired with attempting new actions to further increase knowledge. This is known as the exploitation vs. exploration tradeoff in reinforcement learning
Reinforcement learning
Inspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
.
The model can also be used to control dynamic allocation of resources to different projects, answering the question "which project should I work on" given uncertainty about the difficulty and payoff of each possibility.
Originally considered by Allied scientists in World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
, it proved so intractable that it was proposed the problem be dropped over Germany so that German scientists could also waste their time on it. It was formulated by Herbert Robbins
Herbert Robbins
Herbert Ellis Robbins was an American mathematician and statistician who did research in topology, measure theory, statistics, and a variety of other fields. He was the co-author, with Richard Courant, of What is Mathematics?, a popularization that is still in print. The Robbins lemma, used in...
in 1952.
The multi-armed bandit model
The multi-armed bandit (or just bandit for short) can be seen as a set of real distributions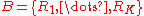, each distribution being associated with the rewards delivered by one of the K levers. Let be the mean values associated with these reward distributions. The gambler iteratively plays one lever per round and observes the associated reward. The objective is to maximize the sum of the collected rewards. The horizon H is the number of rounds that remain to be played. The bandit problem is formally equivalent to a one-state Markov decision processMarkov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
. The regret
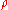after T rounds is defined as the difference between the reward sum associated with an optimal strategy and the sum of the collected rewards: 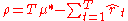, where 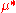is the maximal reward mean, 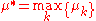, and is the reward at time t. A strategy whose average regret per round 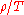tends to zero with probability 1 when the number of played rounds tends to infinity is a zero-regret strategy. Intuitively, zero-regret strategies are guaranteed to converge to an optimal strategy, not necessarily unique, if enough rounds are played.Variations
Another formulation of the multi-armed bandit has each arm representing an independent markov machine. Each time a particular arm is played, the state of that machine advances to a new one, chosen according to the Markov state evolution probabilities. There is a reward depending on the current state of the machine. In a generalisation called the "restless bandit problem", the states of non-played arms can also evolve over time. There has also been discussion of systems where the number of choices (about which arm to play) increases over time.Computer science researchers have studied multi-armed bandits under worst-case assumptions, obtaining positive results for
finite numbers of trials with both
stochastic and nonstochastic arm payoffs.
Common bandit strategies
Many strategies exist which provide an approximate solution to the bandit problem, and can be put into the three broad categories detailed below.Semi-uniform strategies
Semi-uniform strategies were the earliest (and simplest) strategies discovered to approximately solve the bandit problem. All those strategies have in common a greedyGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
behavior where the best lever (based on previous observations) is always pulled except when a (uniformly) random action is taken.
- Epsilon-greedy strategy: The best lever is selected for a proportion
of the trials, and another lever is randomly selected (with uniform probability) for a proportion 
. A typical parameter value might be 
, but this can vary widely depending on circumstances and predilections.
- Epsilon-first strategy: A pure exploration phase is followed by a pure exploitation phase. For
trials in total, the exploration phase occupies 
trials and the exploitation phase 
trials. During the exploration phase, a lever is randomly selected (with uniform probability); during the exploitation phase, the best lever is always selected.
- Epsilon-decreasing strategy: Similar to the epsilon-greedy strategy, except that the value of
decreases as the experiment progresses, resulting in highly explorative behaviour at the start and highly exploitative behaviour at the finish.
- Adaptive epsilon-greedy strategy based on value differences (VDBE): Similar to the epsilon-decreasing strategy, except that epsilon is reduced on basis of the learning progress instead of manual tuning (Tokic, 2010). High changes in the value estimates lead to a high epsilon (exploration); low value changes to a low epsilon (exploitation).
Probability matching strategies
Probability matching strategies reflect the idea that the number of pulls for a given lever should match its actual probability of being the optimal lever.Pricing strategies
Pricing strategies establish a price for each lever. The lever of highest price is always pulled.See also
- Gittins indexGittins indexThe Gittins index is a measure of the reward that can be achieved by a process evolving from its present state onwards with the probability that it will be terminated in future...
— a powerful, general strategy for analyzing bandit problems. - Optimal stoppingOptimal stoppingIn mathematics, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance...
- Search theorySearch theoryIn microeconomics, search theory studies buyers or sellers who cannot instantly find a trading partner, and must therefore search for a partner prior to transacting....
- Greedy algorithmGreedy algorithmA greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
External links
- bandit.sourceforge.net Bandit project , open source implementation of many bandit strategies at sourceforge.net
- Sudipto Guha, Kamesh Munagala, Peng Shi, (2009) "Approximation Algorithms for Restless Bandit Problems", 2009 arXiv:0711.3861v5
- Leslie Pack Kaelbling and Michael L. Littman (1996). Exploitation versus Exploration: The Single-State Case
- Tutorial: Introduction to Bandits: Algorithms and Theory. Part1. Part2.
- Feynman's restaurant problem, a classic example (with known answer) of the exploitation vs. exploration tradeoff.