Gibbs' phase rule
Encyclopedia
Gibbs' phase rule
was proposed by Josiah Willard Gibbs
in the 1870s as the equality
where P (alternatively π or Φ) is the number of phase
s in thermodynamic equilibrium
with each other and C is the number of component
s. Typical phases are solid
s, liquid
s and gas
es. A system involving one pure chemical is an example of a one-component system. Two-component systems, such as mixtures of water and ethanol, have two chemically independent components. F is the number of degrees of freedom
, which means the number of intensive properties such as temperature
or pressure
, which are independent of other intensive variables. This version of the Gibbs' phase rule is only valid for non-reacting systems.
The basis for the rule (Atkins and de Paula, justification 6.1) is that equilibrium between phases places a constraint on the intensive variables. More rigorously, since the phases are in thermodynamic equilibrium with each other, the chemical potential
s of the phases must be equal. The number of equality relationships determines the number of degrees of freedom. For example, if the chemical potentials of a liquid and of its vapour depend on temperature (T) and pressure (p), the equality of chemical potentials will mean that each of those variables will be dependent on the other. Mathematically, the equation μliq(T, p) = μvap(T, p), where μ = chemical potential, defines temperature as a function of pressure or vice versa. (Caution: do not confuse p = pressure with P = number of phases.)
The rule is valid provided the equilibrium between phases is not influenced by gravitational, electrical or magnetic forces, or by surface area, and only by temperature, pressure, and concentration.
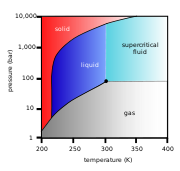In the phase diagram
to the right, the boundary curve between the liquid and gas regions maps the constraint between temperature and pressure when the single-component system has separated into liquid and gas phases at equilibrium. If the pressure is increased by compression, some of the gas condenses and the temperature goes up. If the temperature is decreased by cooling, some of the gas condenses, decreasing the pressure. Throughout both processes, the temperature and pressure stay in the relationship shown by this boundary curve unless one phase is entirely consumed by evaporation or condensation, or unless the critical point
is reached. As long as there are two phases, there is only one degree of freedom, which corresponds to position along the phase line.
The critical point is the black dot at the end of the liquid-gas boundary. As this point is approached, the liquid and gas phases become progressively more similar until, at the critical point, there is no longer a separation into two phases. Above the critical point and away from the phase boundary curve, F = 2 and the temperature and pressure can be controlled independently. Hence there is only one phase, and it has the physical properties of a dense gas, but is also referred to as a supercritical fluid
.
Of the other two-boundary curves, one is the solid–liquid boundary or melting point
curve which indicates the conditions for equilibrium between these two phases, and the other at lower temperature and pressure is the solid–gas boundary.
Even for a pure substance, it is possible that three phases, such as solid, liquid and vapour, can exist together in equilibrium (P = 3). If there is only one component, there are no degrees of freedom (F = 0) when there are three phases. Therefore, in a single-component system, this three-phase mixture can only exist at a single temperature and pressure, which is known as a triple point
. Here there are two equations μsol(T, p) = μliq(T, p) = μvap(T, p), which are sufficient to determine the two variables T and p. In the diagram for CO2 the triple point is the point at which the solid, liquid and gas phases come together, at 5.2 bar and 217 K. It is also possible for other sets of phases to form a triple point, for example in the water system there is a triple point where ice I, ice III
and liquid can coexist.
If four phases of a pure substance were in equilibrium (P = 4), the phase rule would give F = −1, which is meaningless, since there cannot be −1 independent variables. This explains the fact that four phases of a pure substance (such as ice I, ice III, liquid water and water vapour) are not found in equilibrium at any temperature and pressure. In terms of chemical potentials there are now three equations, which cannot in general be satisfied by any values of the two variables T and p, although in principle they might be solved in a special case where one equation is mathematically dependent on the other two. In practice, however, the coexistence of more phases than allowed by the phase rule normally means that the phases are not all in true equilibrium.
As an example, consider the system of two completely miscible liquids such as toluene
and benzene
, in equilibrium with their vapours. This system may be described by a boiling-point diagram which shows the composition (mole fraction) of the two phases in equilibrium as functions of temperature (at a fixed pressure).
Four thermodynamic variables which may describe the system include temperature (T), pressure (p), mole fraction of component 1 (toluene) in the liquid phase (x1L), and mole fraction of component 1 in the vapour phase (x1V). However since two phases are in equilibrium, only two of these variables can be independent (F = 2). This is because the four variables are constrained by two relations: the equality of the chemical potentials of liquid toluene and toluene vapour, and the corresponding equality for benzene.
For given T and p, there will be two phases at equilibrium when the overall composition of the system (system point) lies in between the two curves. A horizontal line (isotherm or tie line) can be drawn through any such system point, and intersects the curve for each phase at its equilibrium composition. The quantity of each phase is given by the lever rule
(expressed in the variable corresponding to the x-axis, here mole fraction).
For the analysis of fractional distillation
, the two independent variables are instead considered to be liquid-phase composition (x1L) and pressure. In that case the phase rule implies that the equilibrium temperature (boiling point
) and vapour-phase composition are determined.
Liquid-vapour phase diagram
s for other systems may have azeotrope
s (maxima or minima) in the composition curves, but the application of the phase rule is unchanged. The only difference is that the compositions of the two phases are equal exactly at the azeotropic composition.
This is sometimes misleadingly called the "condensed phase rule", but it is not applicable to condensed systems which are subject to high pressures (for example in geology), since the effects of these pressures can be important. The rule is useful for some applications in materials science
.
Chapter 9. Thermodynamics Aspects of Stability
was proposed by Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
in the 1870s as the equality
where P (alternatively π or Φ) is the number of phase
Phase (matter)
In the physical sciences, a phase is a region of space , throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, and chemical composition...
s in thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
with each other and C is the number of component
Component (thermodynamics)
In thermodynamics, a component is a chemically distinct constituent ofa system. Calculating the number of components in a system is necessary, for example, when applying Gibbs phase rule in determination of the number of degrees of freedom of a system....
s. Typical phases are solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
s, liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s and gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es. A system involving one pure chemical is an example of a one-component system. Two-component systems, such as mixtures of water and ethanol, have two chemically independent components. F is the number of degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
, which means the number of intensive properties such as temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
or pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, which are independent of other intensive variables. This version of the Gibbs' phase rule is only valid for non-reacting systems.
Foundations
- A phase is a form of matter that is homogeneousHomogeneity (physics)In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
in chemical composition and physical state. Typical phases are solid, liquid and gas. Two immiscibleMiscibilityMiscibility is the property of liquids to mix in all proportions, forming a homogeneous solution. In principle, the term applies also to other phases , but the main focus is usually on the solubility of one liquid in another...
liquids (or liquid mixtures with different compositions) separated by a distinct boundary are counted as two different phases, as are two immiscible solids. - The number of components (C) is the number of chemically independent constituents of the system.
- The number of degrees of freedom (F) in this context is the number of intensive variables which are independent of each other.
The basis for the rule (Atkins and de Paula, justification 6.1) is that equilibrium between phases places a constraint on the intensive variables. More rigorously, since the phases are in thermodynamic equilibrium with each other, the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
s of the phases must be equal. The number of equality relationships determines the number of degrees of freedom. For example, if the chemical potentials of a liquid and of its vapour depend on temperature (T) and pressure (p), the equality of chemical potentials will mean that each of those variables will be dependent on the other. Mathematically, the equation μliq(T, p) = μvap(T, p), where μ = chemical potential, defines temperature as a function of pressure or vice versa. (Caution: do not confuse p = pressure with P = number of phases.)
The rule is valid provided the equilibrium between phases is not influenced by gravitational, electrical or magnetic forces, or by surface area, and only by temperature, pressure, and concentration.
Pure substances (one component)
For pure substances C = 1 so that F = 3 – P. In a single phase (P = 1) condition of a pure component system, two variables (F = 2), such as temperature and pressure, can be controlled to any selected pair of values. However, if the temperature and pressure combination ranges to a point where the pure component undergoes a separation into two phases (P = 2), F decreases from 2 to 1. When the system enters the two-phase region, it becomes no longer possible to independently control temperature and pressure.Phase diagram
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases can occur at equilibrium...
to the right, the boundary curve between the liquid and gas regions maps the constraint between temperature and pressure when the single-component system has separated into liquid and gas phases at equilibrium. If the pressure is increased by compression, some of the gas condenses and the temperature goes up. If the temperature is decreased by cooling, some of the gas condenses, decreasing the pressure. Throughout both processes, the temperature and pressure stay in the relationship shown by this boundary curve unless one phase is entirely consumed by evaporation or condensation, or unless the critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
is reached. As long as there are two phases, there is only one degree of freedom, which corresponds to position along the phase line.
The critical point is the black dot at the end of the liquid-gas boundary. As this point is approached, the liquid and gas phases become progressively more similar until, at the critical point, there is no longer a separation into two phases. Above the critical point and away from the phase boundary curve, F = 2 and the temperature and pressure can be controlled independently. Hence there is only one phase, and it has the physical properties of a dense gas, but is also referred to as a supercritical fluid
Supercritical fluid
A supercritical fluid is any substance at a temperature and pressure above its critical point, where distinct liquid and gas phases do not exist. It can effuse through solids like a gas, and dissolve materials like a liquid...
.
Of the other two-boundary curves, one is the solid–liquid boundary or melting point
Melting point
The melting point of a solid is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at standard atmospheric pressure...
curve which indicates the conditions for equilibrium between these two phases, and the other at lower temperature and pressure is the solid–gas boundary.
Even for a pure substance, it is possible that three phases, such as solid, liquid and vapour, can exist together in equilibrium (P = 3). If there is only one component, there are no degrees of freedom (F = 0) when there are three phases. Therefore, in a single-component system, this three-phase mixture can only exist at a single temperature and pressure, which is known as a triple point
Triple point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...
. Here there are two equations μsol(T, p) = μliq(T, p) = μvap(T, p), which are sufficient to determine the two variables T and p. In the diagram for CO2 the triple point is the point at which the solid, liquid and gas phases come together, at 5.2 bar and 217 K. It is also possible for other sets of phases to form a triple point, for example in the water system there is a triple point where ice I, ice III
Ice III
Ice III is a form of solid matter which consists of tetragonal crystalline ice, formed by cooling water down to at . It is the least dense of the high-pressure water phases, with a density of . The proton-ordered form of is ice IX....
and liquid can coexist.
If four phases of a pure substance were in equilibrium (P = 4), the phase rule would give F = −1, which is meaningless, since there cannot be −1 independent variables. This explains the fact that four phases of a pure substance (such as ice I, ice III, liquid water and water vapour) are not found in equilibrium at any temperature and pressure. In terms of chemical potentials there are now three equations, which cannot in general be satisfied by any values of the two variables T and p, although in principle they might be solved in a special case where one equation is mathematically dependent on the other two. In practice, however, the coexistence of more phases than allowed by the phase rule normally means that the phases are not all in true equilibrium.
Two-component systems
For binary mixtures of two chemically independent components, C = 2 so that F = 4 – P. In addition to temperature and pressure, other variables are the composition of each phase, often expressed as mole fraction or mass fraction of one component.As an example, consider the system of two completely miscible liquids such as toluene
Toluene
Toluene, formerly known as toluol, is a clear, water-insoluble liquid with the typical smell of paint thinners. It is a mono-substituted benzene derivative, i.e., one in which a single hydrogen atom from the benzene molecule has been replaced by a univalent group, in this case CH3.It is an aromatic...
and benzene
Benzene
Benzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6....
, in equilibrium with their vapours. This system may be described by a boiling-point diagram which shows the composition (mole fraction) of the two phases in equilibrium as functions of temperature (at a fixed pressure).
Four thermodynamic variables which may describe the system include temperature (T), pressure (p), mole fraction of component 1 (toluene) in the liquid phase (x1L), and mole fraction of component 1 in the vapour phase (x1V). However since two phases are in equilibrium, only two of these variables can be independent (F = 2). This is because the four variables are constrained by two relations: the equality of the chemical potentials of liquid toluene and toluene vapour, and the corresponding equality for benzene.
For given T and p, there will be two phases at equilibrium when the overall composition of the system (system point) lies in between the two curves. A horizontal line (isotherm or tie line) can be drawn through any such system point, and intersects the curve for each phase at its equilibrium composition. The quantity of each phase is given by the lever rule
Lever rule
The lever rule is a tool used to determine weight percentages of each phase of a binary equilibrium phase diagram. It is used to determine the percent weight of liquid and solid phases for a given binary composition and temperature that is between the liquidus and solidus.-Binary Phase...
(expressed in the variable corresponding to the x-axis, here mole fraction).
For the analysis of fractional distillation
Fractional distillation
Fractional distillation is the separation of a mixture into its component parts, or fractions, such as in separating chemical compounds by their boiling point by heating them to a temperature at which several fractions of the compound will evaporate. It is a special type of distillation...
, the two independent variables are instead considered to be liquid-phase composition (x1L) and pressure. In that case the phase rule implies that the equilibrium temperature (boiling point
Boiling point
The boiling point of an element or a substance is the temperature at which the vapor pressure of the liquid equals the environmental pressure surrounding the liquid....
) and vapour-phase composition are determined.
Liquid-vapour phase diagram
Phase diagram
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases can occur at equilibrium...
s for other systems may have azeotrope
Azeotrope
An azeotrope is a mixture of two or more liquids in such a ratio that its composition cannot be changed by simple distillation. This occurs because, when an azeotrope is boiled, the resulting vapor has the same ratio of constituents as the original mixture....
s (maxima or minima) in the composition curves, but the application of the phase rule is unchanged. The only difference is that the compositions of the two phases are equal exactly at the azeotropic composition.
Phase rule at constant pressure
Condensed systems have no gas phase. When their properties are insensitive to the (small) changes in pressure which occur, one fewer variable needs to be specified, which results in the phase rule at constant pressure- F = C − P + 1 ,
This is sometimes misleadingly called the "condensed phase rule", but it is not applicable to condensed systems which are subject to high pressures (for example in geology), since the effects of these pressures can be important. The rule is useful for some applications in materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
.
Further reading
Mogk, David: Teaching Phase Equilibria. Gibbs' Phase Rule: Where it all Begins (The phase rule in geology)Chapter 9. Thermodynamics Aspects of Stability