
Geopotential model
Encyclopedia
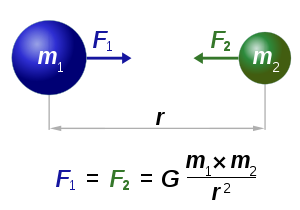
Newton's law of universal gravitation
states that

where:
 As the general three-dimensional body can be considered as the limit of infinitely many infinitely small mass point it follows that the gravitational force attracting the mass point to the three-dimensional body per unit mass of the mass point is the integral over the volume
As the general three-dimensional body can be considered as the limit of infinitely many infinitely small mass point it follows that the gravitational force attracting the mass point to the three-dimensional body per unit mass of the mass point is the integral over the volume
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
states that
- Every point mass attracts every single other point mass by a forceForceIn physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
pointing along the lineLine (mathematics)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
intersecting both points. The force is proportionalProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the productProduct (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of the two massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
es and inversely proportionalProportionality (mathematics)In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the square of the distance between them.

where:
- F is the force between the masses,
- G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, - m1 is the first mass,
- m2 is the second mass, and
- r is the distance between the masses.

-
with corresponding potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
-
where- G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, -
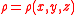 is the mass density at the volume element,
is the mass density at the volume element, -
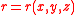 is the distance between the mass point and the volume element
is the distance between the mass point and the volume element -
 is the unit vector of the direction from the volume element to the point mass
is the unit vector of the direction from the volume element to the point mass
The case of a homogeneous sphere
In the special case of a sphere with a spherically symmetric mass density (for example a constant mass density!)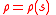
where these integrals can be evaluated analytically. This is the shell theoremShell theoremIn classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
these integrals can be evaluated analytically. This is the shell theoremShell theoremIn classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
saying that in this case:
-
with corresponding potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
-
where-
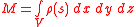 is the total mass of the sphere
is the total mass of the sphere -
 is the distance between the mass point and the center of the sphere
is the distance between the mass point and the center of the sphere -
 is the unit vector of the direction from the center of the sphere to the point mass
is the unit vector of the direction from the center of the sphere to the point mass
The deviations of the gravitational field of the Earth from that of homogeneous sphere
In reality the shape of the Earth is not exactly spherical, mainly because of its rotation around the polar axis what makes its shape slightly oblate. If this shape would have been perfectly known together with the exact mass density the integrals and could have been evaluated with numerical methods to find a more accurate model for the gravitational field of the Earth. But the situation is in fact the opposite, by observing the orbits of spacecraft (and the Moon) the gravitational field of the Earth can be determined quite accurately and the best estimate of the mass of the Earth is obtained by dividing the product
the integrals and could have been evaluated with numerical methods to find a more accurate model for the gravitational field of the Earth. But the situation is in fact the opposite, by observing the orbits of spacecraft (and the Moon) the gravitational field of the Earth can be determined quite accurately and the best estimate of the mass of the Earth is obtained by dividing the product  as determined from the analysis of spacecraft orbit with a value for
as determined from the analysis of spacecraft orbit with a value for  determined to a lower relative accuracy using other physical methods.
determined to a lower relative accuracy using other physical methods.
From the defining equations and it is anyway clear (taking the partial derivatives of the integrand) that outside the body in empty space the following differential equations are valid for the field caused by the body:-
-
Functions satisfying the partial differential equation (the Laplace equationLaplace's equationIn mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
) are called harmonic functions.
The functions-
where
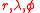 are the spherical coordinates
are the spherical coordinates
-
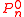 are the Legendre polynomials
are the Legendre polynomials
and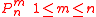 are the associated Legendre functionsAssociated Legendre polynomialsIn mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
are the associated Legendre functionsAssociated Legendre polynomialsIn mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
satisfy the partial differential equation and are consequently "harmonic". They are called the spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
The first spherical harmonics with n=0,1,2,3 are

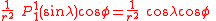
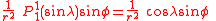
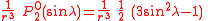
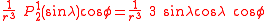
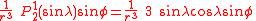
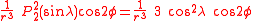
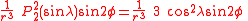


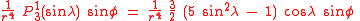
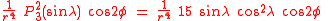
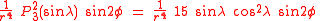


The model for the Earth gravitational field is that its potential is a sum
-
where the coordinates are relative the standard geodetic reference system extended into space with origin in the center of the reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
and with z-axis in the direction of the polar axis.
The terms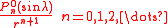
are called the zonal terms
and the terms
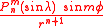
are called the tesseral terms
The zonal and tesseral terms for n = 1 are left out in !
The different coefficients
are then given the values for which the best possible agreement between the computed and the observed spacecraft orbits is obtained.
As for odd indexes n non-zero coefficients
for odd indexes n non-zero coefficients 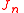 for odd n correspond to a lack of symmetry "north/south" relative the equatorial plane for the shape/mass-distribution of the Earth. Non-zero coefficients
for odd n correspond to a lack of symmetry "north/south" relative the equatorial plane for the shape/mass-distribution of the Earth. Non-zero coefficients  correspond to a lack of rotational symmetry around the polar axis for the shape/mass-distribution of the Earth, i.e. to a "tri-axiality" of the Earth
correspond to a lack of rotational symmetry around the polar axis for the shape/mass-distribution of the Earth, i.e. to a "tri-axiality" of the Earth
For large values of n the coefficients above (that are divided by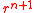 in ) take very large values when for example kilometers and seconds are used as units. In the literature it is common to introduce some arbitrary "reference radius"
in ) take very large values when for example kilometers and seconds are used as units. In the literature it is common to introduce some arbitrary "reference radius"  close to the radius of the Earth and to work with the dimensionless coefficients
close to the radius of the Earth and to work with the dimensionless coefficients

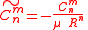
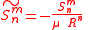
and to write the potential as
-
The (by far) dominating term (after the term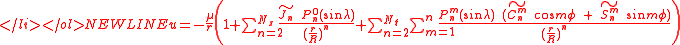 ) in is the "
) in is the "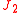 term":
term":

Relative the coordinate system-
illustrated in figure 1 the components of the force caused by the " term" are
term" are
-
In the rectangular coordinate system
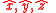
the force components are:-
The components of the force corresponding to the "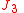 term"
term"

are-
and
-
The exact numerical values for the coefficients deviate (somewhat!) between different Earth models but for the lowest coefficients they all agree almost exactly.
For JGM-3 the values are:

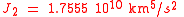

With a "reference radius" of 6378.1363 km corresponding dimensionless parameters are
of 6378.1363 km corresponding dimensionless parameters are

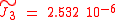
At a radius of for example 6600 km (about 200 km over the Earth surface)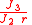 is about 0.002, i.e
is about 0.002, i.e
the correction to the "J2 force" from the "J3 term" is in the order of 2 promille. The negative value of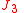 implies that for a mass point in the equatorial plane of the Earth the gravitational force is tilted slightly towards south due to the lack of symmetry for the mass distribution of the Earth "north/south".
implies that for a mass point in the equatorial plane of the Earth the gravitational force is tilted slightly towards south due to the lack of symmetry for the mass distribution of the Earth "north/south".
Available models
The earliest Earth models in general use by NASANASAThe National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
and ESROESROThe European Space Research Organization was an international organisation founded by 10 European nations with the intention of jointly pursuing scientific research in space. It was founded in 1964...
/ESA were the "Goddard Earth Models" developed by Goddard Space Flight CenterGoddard Space Flight CenterThe Goddard Space Flight Center is a major NASA space research laboratory established on May 1, 1959 as NASA's first space flight center. GSFC employs approximately 10,000 civil servants and contractors, and is located approximately northeast of Washington, D.C. in Greenbelt, Maryland, USA. GSFC,...
denoted "GEM-1", "GEM-2", "GEM-3", and so on. Later the "Joint Earth Gravity Models" denoted "JGM-1", "JGM-2", "JGM-3" developed by Goddard Space Flight CenterGoddard Space Flight CenterThe Goddard Space Flight Center is a major NASA space research laboratory established on May 1, 1959 as NASA's first space flight center. GSFC employs approximately 10,000 civil servants and contractors, and is located approximately northeast of Washington, D.C. in Greenbelt, Maryland, USA. GSFC,...
in cooperation with universities and private companies became available. The newer models generally provided higher order terms than their precursors. The EGM96EGM96EGM96 is a geopotential model of the Earth consisting of spherical harmonic coefficients complete to degree and order 360...
uses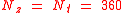 resulting in 130317 coefficients.
resulting in 130317 coefficients.
For a normal Earth satellite for which an orbit determination/prediction accuracy of a few meters is sufficient the "JGM-3" truncated to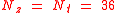 (1365 coefficients) is usually sufficient. Inaccuracies from the modeling of the air-drag and to a lesser extent the solar radiation pressure will exceed the inaccuracies caused by the gravitation modeling errors.
(1365 coefficients) is usually sufficient. Inaccuracies from the modeling of the air-drag and to a lesser extent the solar radiation pressure will exceed the inaccuracies caused by the gravitation modeling errors.
Spherical harmonics
(Main article Spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
)
The following is a compact account of the spherical harmonics used to model the gravitational field of the Earth using the precisely the same notations as above:
The spherical harmonics are derived from the approach of looking for harmonic functions of the form
-
where
 are the spherical coordinates defined by the equations
are the spherical coordinates defined by the equations
By straightforward calculations one gets that for any function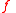
-
Introducing the expression in one gets that
-
As the term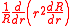
only depends on the variable and the sum
and the sum
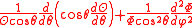
only depends on the variables and
and 
one gets that is harmonic if and only if
is harmonic if and only if
-
and-
for some constant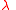
From then follows that

The first two terms only depend on the variable and the third only on the variable
and the third only on the variable  .
.
From the definition of as a spherical coordinate it is clear that
as a spherical coordinate it is clear that 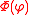 must be periodic with the period
must be periodic with the period  and one must therefore have that
and one must therefore have that
-
and-
for some integer as the family of solutions to then are
as the family of solutions to then are
-
With the variable substitution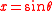
equation takes the form
-
From follows that in order to have a solution with
with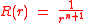
one must have that
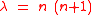
If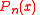 is a solution to the differential equation
is a solution to the differential equation
-
one therefore has that the potential corresponding to m=0
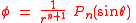
which is rotational symmetric around the z-axis is an harmonic function
If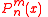 is a solution to the differential equation
is a solution to the differential equation
-
with one has that the potential
one has that the potential
-
where a and b are arbitrary constants is a harmonic function that depends on and therefore is not rotational symmetric around the z-axis
and therefore is not rotational symmetric around the z-axis
The differential equation is the Legendre differential equation for which the Legendre polynomials defined-
are the solutions
The arbitrary factor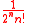 is selected to make
is selected to make 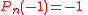 and
and  for odd n and
for odd n and 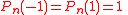 for even n.
for even n.
The first six Legendre polynomials are:
-
The solutions to differential equation are the associated Legendre functions-
One therefore has that

External links
- http://cddis.nasa.gov/lw13/docs/papers/sci_lemoine_1m.pdf
- http://geodesy.eng.ohio-state.edu/course/refpapers/Tapley_JGR_JGM3_96.pdf
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- G is the gravitational constant
-

